Si ara volem determinar l'àrea que delimiten dues funcions:
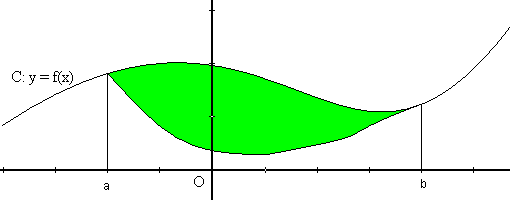
descompondrem el problema en dues parts: primer calcularem l'àrea delimitada per la gràfica superior amb l'eix i llavors li restarem l'àrea delimitada per la gràfica inferior.
És a dir, si la gràfica superior és $$(x,f(x))$$ i la inferior és $$(x,g(x))$$: $$$ A=\int_a^b f(x) \ dx - \int_a^b g(x) \ dx$$$
Calculem l'àrea delimitada per les funcions $$f(x)=\sin\Big( \dfrac{\pi}{2} \Big)$$ i $$g(x)=x$$ en l'interval $$[0,1]$$. Dibuixem les funcions per saber quina és la gràfica superior i quina la inferior:
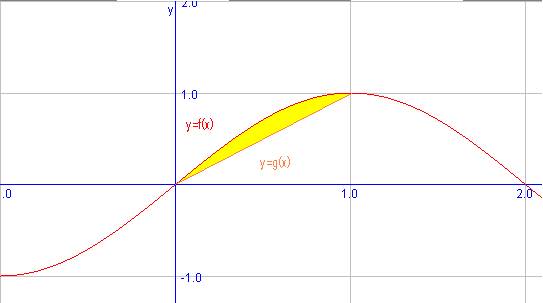
Així, veiem que la gràfica superior és $$f(x)$$ i la inferior és $$g(x)$$. Per tant l'àrea entre les dues funcions entre $$[-1,1]$$ és:
$$$ \begin{array}{rl} A =&\int_0^1 f(x)\ dx-\int_0^1 g(x) \ dx = \int_0^1 \sin\Big(\dfrac{\pi}{2}x\Big) \ dx- \int_0^1 x \ dx \\ =& \dfrac{2}{\pi}\Big[-\cos\Big(\dfrac{\pi}{2}x \Big)\Big]_0^1-\Big[\dfrac{x^2}{2}\Big]_0^1= \dfrac{2}{\pi}(0+1)-\dfrac{1}{2}=\dfrac{4-\pi}{2\pi}u^2 \end{array}$$$
