Una funció polinòmica és una funció on l'expressió analítica ve donada per un polinomi: $$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$$$ amb $$n \in \mathbb{N}\cup \{0\}$$, $$a_n,a_{n-1},\ldots, a_1,,_a0 \in \mathbb{R}$$ i $$a_n\neq 0$$ si $$n\neq 0$$.
Com els polinomis poden ser avaluats en qualsevol nombre real, tenim que el domini de les funcions polinòmiques és tot $$\mathbb{R}$$, és a dir, $$Dom(f)=\mathbb{R}$$.
La imatge d'aquest tipus de funcions no sempre és evident:
- Polinomi de grau senar: Aquest és el cas senzill ja que $$Im(f)=\mathbb{R}$$.
- Polinomi de grau parell: La imatge dependrà dels coeficients del polinomi, que determinaran orientació i extrems relatius. En el cas $$n = 2$$, és a dir funcions quadràtiques, només cal conèixer el vèrtex de la paràbola i tenir en compte la seva orientació.
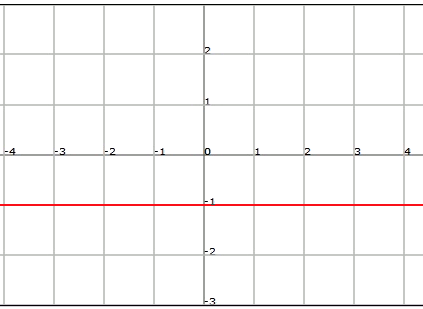
Funció constant: $$f (x) = k$$
Es tracta d'una funció polinòmica de grau $$0$$. La seva gràfica és una recta horitzontal que passa per tots els punts d'ordenada $$y=k$$ (i per tant $$Im (f) = k$$).
Un exemple de funció constant és $$f (x) =-1$$:
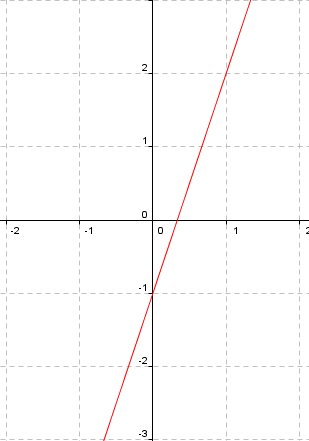
Funció afí: $$f (x) = ax + b$$
Un requisit és que sigui $$a\neq 0$$. Es tracta d'una funció polinòmica de grau $$1$$. La seva gràfica és una recta que passa pel punt $$(0, b)$$ i la inclinació depèn del valor de $$a$$ (també conegut com pendent).
En el cas particular en què $$b = 0$$, es té la coneguda com a funció lineal: $$f (x) = ax$$. Aquesta funció és equivalent a la funció de proporcionalitat directa, on $$a$$ és la constant de proporcionalitat.
En el cas particular en què $$a = 1$$, obtenim la funció identitat, és a dir, $$f (x) = x$$ , la gràfica de la qual és la bisectriu del primer i del tercer quadrant.
Vegem un exemple: $$f (x) = 3x - 1$$.
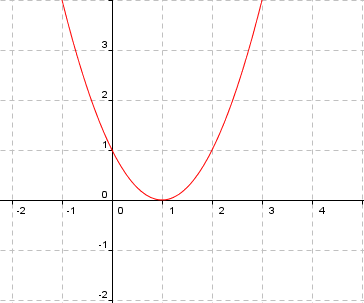
Funció quadràtica: $$f (x) = ax^2 + bx + c$$
Per obtenir una funció quadràtica és necessari que $$a\neq 0$$. Es tracta d'una funció polinòmica de segon grau, la gràfica és una paràbola oberta cap amunt si $$a> 0$$, o bé cap avall si $$a <0$$.
El vèrtex d'aquesta paràbola és $$\displaystyle \Big(-\frac{b}{2a}, -\frac{b^2-4ac}{4a}\Big)$$.
El punt de tall amb l'eix vertical és $$c$$. Els punts de tall amb l'eix horitzontal són les solucions de l'equació de segon grau corresponent.
Un exemple de funció quadràtica és $$f(x) =x^2-2x+1$$.
