Una fracció és una quantitat dividida per una altra quantitat. I una unitat fraccionaria és cadascuna de les parts que s'obtenen al dividir una unitat. Però per a veure amb claredat aquests conceptes anem a fer la construcció següent.
Prenem un objecte qualsevol, podria ser un pastís, un llapis, una pizza o fins i tot una taula, però anem a utilitzar un quadrat blau:
A continuació partirem aquest quadrat en quatre parts iguals:
I d'aquestes quatre parts anem a pintar una d'elles de vermell:
D'aquesta manera podem definir la fracció que correspon a la part vermella, i ho farem dient que el quadradet vermell és una quarta part del quadrat blau original. És a dir, escrivim la fracció del rectangle de color vermell com:
$$\dfrac{1}{4}=\dfrac{\mbox{part del quadrat que està pintada de vermell}}{\mbox{número de parts del quadrat}}$$
De la mateixa manera podríem considerar el quadrat en sis parts iguals:
I d'aquestes sis, pintar de vermell quatre d'elles:
Llavors escrivim la fracció del rectangle en vermell com:
$$\dfrac{4}{6}=\dfrac{\mbox {parts del quadrat que estan en vermell}}{\mbox{número de parts del quadrat}}$$
Sempre escriurem les fraccions amb aquesta forma: el nombre de parts escollides, sobre una ratlla, amb el número de parts totals sota. I per llegir, primer diem el nombre de dalt i a continuació el de sota indicant-ho amb un partit, és a dir:
u partit per dos (una meitat) serà: $$\dfrac{1}{2}$$
tres partit per deu: $$\dfrac{3}{10}$$
onze partit per sis: $$\dfrac{11}{6}$$
També, si la fracció és partida per dos, parlem de meitats o mitjos, entre tres parlem de terços, i a partir de quart parlem de quarts, cinquens, etc.:
tres mitjos: $$\dfrac{3}{2}$$
cinc onzens: $$\dfrac{5}{11}$$
set onzens: $$\dfrac{7}{11}$$
Observem que el segon número és el que dóna nom a la fracció indicant-nos si són mitjans, terços o vuitens, per aquest motiu l'anomenem denominador, perquè ens dóna nom a la fracció: la denomina.
D'altra banda, el primer número ens explica el nombre de parts escollides (pintades de vermell) que tenim, és a dir ens numera les diferents fraccions amb el mateix denominador, per això en diem numerador.
$$$\displaystyle \begin{array}{rcl} \underline{2} & \leftarrow & numerador \\ 3 &\leftarrow & denominador\end{array}$$$
Considerem ara la fracció representada pel dibuix següent:
Les parts en color gris es poden expressar com 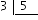$$\dfrac{3}{5}$$ és a dir, tres cinquens. Aquest tipus d'operació és equivalent a la divisió:
Per a veure-ho més clar, comencem per la fracció un cinquè: $$\dfrac{1}{5}$$.
Com ja hem vist gràficament, aquesta fracció equival a retallar un rectangle en cinc parts iguals i d'aquestes agafar-ne una.
És a dir, dividir un quadrat entre 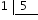$$5$$, $$\dfrac{1}{5}$$, equival a fer la divisió
En el cas de tenir tres cinquens: 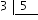$$\dfrac{3}{5}$$, ja hem dividit el rectangle en cinc parts però hem agafat tres, per això, 
Tota divisió es pot escriure com una fracció, així com qualsevol fracció es pot escriure com divisió, però és important que en escriure les fraccions, els numeradors i els denominadors no poden ser nombres decimals ni arrels. És a dir, numerador i denominador han de ser sempre nombres enters.
$$\dfrac{9.5}{3}, \dfrac{\sqrt{3}}{4}, \dfrac{2}{1.9}, \dfrac{6}{\sqrt{33}}$$ no seran fraccions. En canvi:
$$\dfrac{-7}{2},\dfrac{8}{5}, \dfrac{-1}{-2}$$ sí seran fraccions.
Segons això es podria pensar que el número 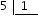$$5$$ no hauria de ser una fracció, però sí que ho és atès que la fracció equival a la divisió 
, que si la resolem ens dóna:
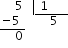
Per tant: $$$\dfrac{5}{1}=5$$$
D'igual forma, a qualsevol nombre enter se li pot assignar una fracció el denominador de la qual és $$1$$.
Ara estem preparats per a donar una definició formal de fracció.
Definició: Si $$a$$ i $$b$$ són dos nombres enters tals que $$b\neq0$$, anomenarem fracció a l'expresió $$\frac{a}{b}$$ en la que $$a$$ és el numerador i $$b$$ el denominador i que equival al quocient de la divisió de $$a$$ entre $$b$$.
La principal utilitat de les fraccions és expressar parts d'un total.
Vegem un exemple per a començar:
Volem expressar cadascún dels temps d'un partit de fútbol. Cada temps és de tres quarts d'hora i escrivim $$\dfrac{3}{4}$$h.
Per a saber què significa tenir $$\dfrac{3}{4}$$h hem de dividir la hora en quatre parts i prendre'n tres. Com que sabem que una hora són $$60$$ minuts, partim $$60$$ entre $$4$$. Obtenim $$15$$. És a dir, una quarta part de $$60$$ és $$15$$. Així doncs, un quart d'hora són $$15$$ minuts.
Per obtenir el que valen els tres quarts d'hora, hem de multiplicar un quart d'hora per tres: d'aquesta forma $$\dfrac{3}{4}$$h són $$15\cdot3=45$$ minuts.
En general, si volem calcular $$\dfrac{n}{m}$$ d'una quantitat $$x$$ (amb $$m\neq0$$ necessàriament) hem de fer aquesta cadena d'operacions: $$(x:m)\cdot n$$
Com ja hem vist a l'exemple de les hores, $$\dfrac{3}{4}$$ d'hora són $$45$$ minuts, ja que, al ser $$1$$h$$=60$$min, fem: $$$(60:4)\cdot3=(15)\cdot3=15\cdot3=45 \text{ minuts. }$$$
Volem fer un pou amb una profunditat de $$30$$m per sota del nivell de terra: és a dir, una alçada de $$-30$$m. Quan hem perforat exactament $$\dfrac{2}{3}$$ del pou, ens trobem una pedra que ens impedeix continuar la perforació. Volem saber a quants metres de profunditat l'hem trobat.
Per calcular-ho dividim els $$-30$$m entre $$3$$ i multipliquem el resultat per $$2$$: $$$(-30:3)\cdot2=-10\cdot2=-20\text{ m. }$$$ És a dir, hem trobat la pedra a $$20$$ metres de profunditat.