Increasing and decreasing functions
The functions can be increasing or decreasing along its domain or in a certain interval.
We say that a function $$f(x)$$ is increasing in the interval $$[a,b]$$ if given any two points in $$[a,b]$$, $$x_1$$ and $$x_2$$ such that $$x_1 < x_2$$ then $$f(x_1) \leqslant f(x_2)$$.
We say that a function $$f(x)$$ is decreasing in the interval $$[a,b]$$ if given any two points in $$[a,b]$$, $$x_1$$ and $$x_2$$ such that $$x_1 < x_2$$ then $$f(x_1) \geqslant f(x_2)$$.
The functions that never decrease, they always increase in value or remain the same (the increasing functions).
Similarly, the decreasing functions never increase, they always decrease in value or they remain the same when $$x$$ becomes bigger.
On the other hand, we can define definitely increasing or decreasing functions: these will never be supported in the same value, or else they increase or diminish.
We say that a function $$f(x)$$ is strictly increasing in the interval $$[a,b]$$ if given two points in $$[a,b]$$, $$x_1$$ and $$x_2$$ such that $$x_1 < x_2$$ then $$f(x_1) < f(x_2)$$.
We say that a function $$f(x)$$ is strictly decreasing in the interval $$[a,b]$$ if given two points in $$[a,b]$$, $$x_1$$ and $$x_2$$ such that $$x_1 < x_2$$ then $$f(x_1) > f(x_2)$$.
Next we will see a few examples:
All the functions of the type $$f(x)=ax+b$$ whith $$a>0$$ are increasing functions, and in particular, they are strictly increasing functions. Nevertheless, when we take $$a < 0$$ we will obtain strictly decreasing functions (and consequently decreasing).
The function $$f(x)=x^2$$ is a decreasing function in the interval $$(-\infty,0]$$ and increasing in $$[0,+\infty)$$.
The constant functions are functions that are simultaneously increasing and decreasing (they stay constant).
Maximums and minimums
When we represent a function we can sometimes see that we have points that are relative or absolute maximums or minimums.
As we can see in the following example the function $$f(x)=x^2$$ has an absolute minimum at $$x=0$$:
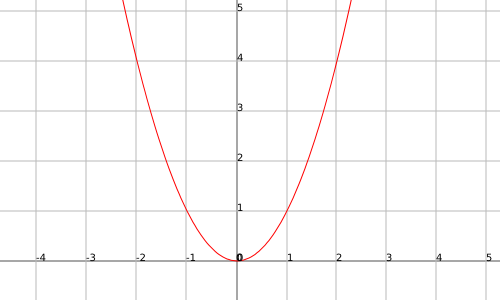
Let's correctly define the concept of relative and absolute maximum and minimum:
- A point $$x_0$$ is named a global maximum if for any point $$x$$ of the domain, the function satisfies $$f(x)\leqslant f(x_0)$$.
- A point $$x_0$$ is named a global minimum if for any point $$x$$ of the domain, the function satisfies $$f(x)\geqslant f(x_0)$$.
- A point $$x_0$$ is named a relative maximum if for any point $$x$$ of an environment of $$x_0$$ $$\ [x_0-\varepsilon,x_0+\varepsilon]$$ (where $$\varepsilon$$ is a small value), the function satisfies $$f(x)\leqslant f(x_0)$$.
- A point $$x_0$$ is named a relative minimum if for any point $$x$$ of an environment of $$x_0$$ $$\ [x_0-\varepsilon,x_0+\varepsilon]$$ (where $$\varepsilon$$ is a small value), the function satisfies + $$f(x)\geqslant f(x_0)$$.
To better understand these concepts let's see an example for each one:
The function $$f(x)=x^2$$ presents a global minimum in the point $$x=0$$ (see the example previous to the definitions).
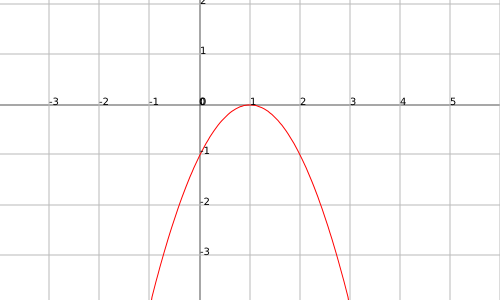
The function $$f(x)=-(x-1)^2$$ presents a global maximum in the point $$x=1$$:
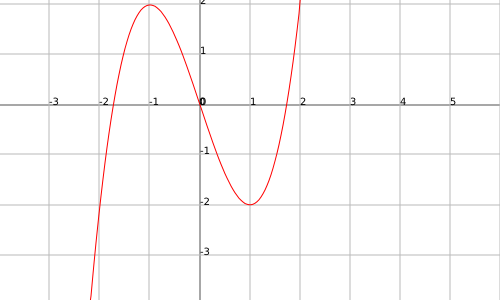
The function $$f(x)=x^3-3x$$ presents a relative maximum in $$x=-1$$ and a relative minimum in $$x=1$$:
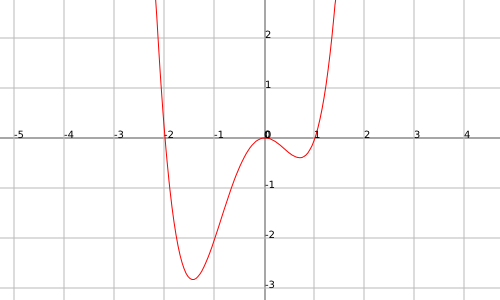
The function $$f(x)=x^4-x^3-2x^2$$ presents a global minimum somewhere in the interval $$[-2, -1]$$, has a relative maximum in $$x=0$$ and a relative minimum somewhere in the interval $$(0,1)$$:
Location of maximums and minimums
We are going to find maximums and relative minimums.
To do so, we consider a continuous function $$f(x)$$ in an open and derivable domain.
If we concentrate on the previous graphs, we see that the tangent line on the maximums and minimums points are horizontal, so they have slope equal to zero.
The procedure will be to derive the function $$f(x)$$ and equate it to zero. Solving the equation, we obtain we will find the points $$x$$ that will be maximums or minimums of our function. The following step will be to know if they are maximum or minimum.
This can be deduced from the value of the second derivative of the function at the point we just found: if it is positive, it will be a minimum, and if it is negative, it will be maximum.
To clearly understand the process, let's see an example.
Let's take the function $$f(x)=x^3-3x$$.
We will start by deriving the function and equaling it to zero. We will solve the equation and will obtain the solution points. $$$f'(x)=3x^2-3 \Rightarrow 3x^2-3=0 \Rightarrow x^2=1 \Rightarrow x=\pm1$$$
Now we know that in the points $$1$$ and $$-1$$ we have maximums or minimums. We are going to see what are they by using the second derivative, $$f''(x)=6x$$:
$$f''(1)=6 > 0$$
$$f''(-1)=-6 < 0$$
And consequently we have maximum in $$x =- 1$$ and we have a minimum in $$x = 1$$.
Let's see the graph:

