Optimitzation

A public garden has a triangular form, and the sides measure $$4 \ m$$ and $$12 \ m$$ respectively. In this public garden we want to construct a playground, but the regulation says it must be rectangular. What is it the maximum area that the playground will have? Or, similarly, what is the biggest rectangle that we can be formed within a triangle whereby the sides of the rectangle are $$4\ m$$ and $$12\ m$$?

Step 1: Comprehension of the problem.

A drawing / scheme of the problem is normally useful.

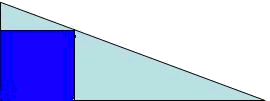
Step 2: Construct the function.

One must identify the quantity to maximize or to minimize and to be able to write it mathematically. In this case one should maximize the area of the rectangle. Therefore, if we call $$x$$ the length and $$y$$ the width, the function area $$A$$ will be:

$$$A=x\cdot y$$$

Step 3: Find relationships that allow us to write the function area with only one unknown.

Here we can be use the resemblance of the triangles (theorem of Thales).

$$$\dfrac{4-y}{x}=\dfrac{4}{12} \Rightarrow x=3(4-y)$$$

Step 4: Rewrite the function, now with only one variable.

We change the value of $$x$$ by its dependence on $$y$$, rewriting the value of $$A=x\cdot y$$

$$$A(y)=3\cdot(4-y)\cdot y=-3y^2+12y$$$

Step 5: Maximize (or minimize).

We will set the derivative of the function equal to zero and obtain the value of the variable.

$$$A'(y)=-6y+12=0 \Rightarrow y=2$$$

Step 6: Find the value of other involved variables.

The solution has been $$y=2\ m$$. We use what we know about the dependence on $$x$$ of $$y$$ to find the value of $$x$$.

$$$\left.\begin{array}{c}x=3(4-y)\\y=2\end{array}\right\}\Rightarrow x=6\ m$$$

Step 7: Give the result.

The biggest playground in this area will have dimensions of $$6\times2$$ meters, therefore the area will be $$12\ m^2$$.

Determine the minimal distance from the point $$(0,1)$$ up to the parabola $$y=x^2$$.

Step 1: Comprehension of the problem.

We want to find the distance between a parabola centred on the origin $$(0,0)$$ and the point $$(0,1)$$. We could do a drawing to facilitate comprehension.

Step 2: Construct the function.

We must minimize the distance, which we will call $$d$$.

The distance function - using Pythagoras' theorem - between points $$(0,1)$$ and $$(x,y)$$ which are the coordinates of any of the points of the parabola.

Then,

$$$d^2=(0-x)^2+(1-y)^2\Rightarrow d=\sqrt{x^2+(1-y)^2}$$$

Step 3: Find relationships that allow us to write the function area with only one unknown.

In this case we know that $$y=x^2$$.

Step 4: Rewrite the function, now with just one variable.

The function becomes $$d(x)=\sqrt{x^2+(1-x^2)^2}$$

Step 5: Maximize (or minimize).

We will set the derivative of the function equal to zero and obtain the value of the variable. (See item for calculating derivatives if necessary)

$$$d'(x)=\dfrac{1}{2}\ \dfrac{\ 2x+2(1-x^2)(-2x)\ }{\sqrt{x^2+(1-x^2)^2}}=0$$$

If we continue with the calculation,

$$$2x-4x(1-x^2)=0\Rightarrow \left\{ \begin{array}{cc}x=0\ , & \ \\x=\dfrac{\sqrt{2}}{2} & \ \ \ \mbox{or}\ \ \ \ x=-\dfrac{\sqrt{2}}{2}\end{array}\right.$$$

Step 6: Find the value of the other variables involved.

Every value of $$x$$ has a value an associate of $$y \ \ $$ ($$y=x^2$$)

$$$x=0\ \ \ \Rightarrow \ y=0$$$

$$$x=\dfrac{\sqrt{2}}{2}\ \Rightarrow \ y=\dfrac{1}{2}$$$

$$$x=-\dfrac{\sqrt{2}}{2}\ \Rightarrow y=\dfrac{1}{2}$$$

Step 7: Get the result.

In this case there are three points placed at the same distance, which is the minimal distance. These three points are:

$$$\left(-\dfrac{\sqrt{2}}{2},\dfrac{1}{2}\right)\ \ ;\ \ \left(0,0\right)\ \ ;\ \ \left(\dfrac{\sqrt{2}}{2},\dfrac{1}{2}\right)$$$

For all of them $$d=1$$, which is a way to check if these three points are really at the same distance and that there are no errors in the calculations.