Elementos de la raíz cuadrada
Cuando resolvemos la raíz cuadrada con su método de resolución usual debemos conocer las partes en las que se divide la raíz cuadrada a medida que se procede. Las partes de las que se compone son:
- Radical, es el símbolo que indica que es una raíz cuadrada.
- Radicando, es el número del que se obtiene la raíz cuadrada.
- Raíz, es propiamente la raíz cuadrada del radicando.
- Renglones auxiliares, nos ayudaran a resolver la raíz cuadrada.
- Resto, es el número final del proceso para resolver la raíz cuadrada.
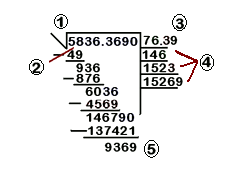
Cálculo de la raíz cuadrada paso a paso
Cuando se calcula la raíz cuadrada de un número se debe ser consciente que el resultado puede no ser un número natural, sino un número decimal. Estudiaremos el cálculo de la raíz cuadrada con solución números naturales.
Para calcular la raíz cuadrada de un número de varias cifras se procede así:
-
Se divide el número en grupos de dos cifras empezando por la derecha.
-
Se calcula el número que multiplicado por él mismo es más próximo pero no excede del primer grupo de cifras de la izquierda y así se obtiene la primera cifra de la raíz que ponemos a la derecha del radicando, en el primer renglón auxiliar. Entonces el cuadrado de esta cifra se resta del primer grupo.
-
A la derecha del resto obtenido se escribe el segundo grupo y se separa la cifra de la derecha.
-
El número que queda a la izquierda de la cifra separada se divide por el doble de la raíz obtenida. El cociente se escribe a la derecha del divisor y la parte entera del número que resulta de la división se multiplica por el mismo cociente. Si este producto se puede restar del dividendo seguido de la cifra separada, el cociente es la cifra de la raíz, sino es así se prueba con una cifra inferior.
- Se repiten los pasos 3º y 4º hasta que no quede ningún grupo del radicando por bajar.
Ejemplo
Hagámoslo primero con una cifra que sea un cuadrado perfecto:
Busquemos la raíz de
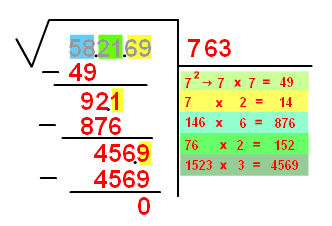
Paso a paso sería:
1) Se separan de
| 58.21.69 |
2) Se busca un número que elevado al cuadrado dé próximo a
| 58.21.69 | 7 |
| 7·7=49 |
3) Se resta ese resultado de
| 58.21.69 | 7 |
| -49 | 7·7=49 |
| 92.1 |
4) Ponemos el doble de
En este caso es
Restamos, bajamos las siguientes dos cifras y separamos la última (ahora un
| 58.21.69 | 76 |
| -49 | 7·7=49 |
| 92.1 | 7·2=14 |
| -876 | 146·6=876 |
| 456.9 |
5) Hacemos lo mismo que en el paso anterior. Es decir, multiplicamos
Cuando se restan da cero y por lo tanto no hace falta seguir.
Ponemos el
| 58.21.69 | 763 |
| -49 | 7·7=49 |
| 92.1 | 7·2=14 |
| -876 | 146·6=876 |
| 456.9 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 0 |
La raíz cuadrada de
Veamos ahora un ejemplo de un número que no es un cuadrado perfecto, sino un número decimal:
Ejemplo
La raíz de
1) Se separa el número del radicando en grupos de dos cifras. La separación se hace desde el signo de decimal (si lo hay) hacia la derecha y hacia la izquierda.
Si en el lado de los decimales no hay un número par de cifras, es evidente que queda una suelta: en ese caso, le añadimos un cero.
Si en el lado de los enteros nos quedara un número suelto, se quedaría así. En nuestro caso debemos añadir un cero al lado del
| 58.36,36.90 |
2) Buscamos un número que multiplicado por sí mismo de como resultado el número que coincida o que más se aproxime por debajo a
En este caso el número sería el
| 58.36,36.90 | 7 |
| 7·7=49 |
3) Restamos
| 58.36,36.90 | 7 |
| -49 | 7·7=49 |
| 93.6 |
4) Ponemos el doble de
Restamos, bajamos las siguientes dos cifras y separamos la última. En este caso bajamos
Puesto que éstas están a la derecha del punto decimal, en el primer renglón donde vamos escribiendo la raíz cuadrada se le pone un punto decimal también. Escrito será:
| 58.36,36.90 | 76, |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 |
5) Ahora, hacemos lo mismo que en el paso anterior. Es decir, multiplicamos
La operación a realizar por lo tanto es
Bajamos después las siguientes dos cifras. También ponemos el
| 58.36,36.90 | 76,3 |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 1467.90 |
6) Volvemos a hacer lo mismo. Multiplicamos la raíz que tenemos escrita por el momento
El resultado se agrega al siguiente renglón auxiliar, y se vuelven a dividir los primeros cuatro números del residuo
El nueve se pone en el renglón de la raíz y se multiplica
| 58.36,36.90 | 76,3 |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 1467.90 | 763·2=1526 |
| -137421 | 15269·9=137421 |
| 9369 |
En este momento, podemos escribir que aproximadamente se tiene que la raíz cuadrada de
La operación anterior utilizada como ejemplo no está completa. Si la continuáramos daría como resultado

