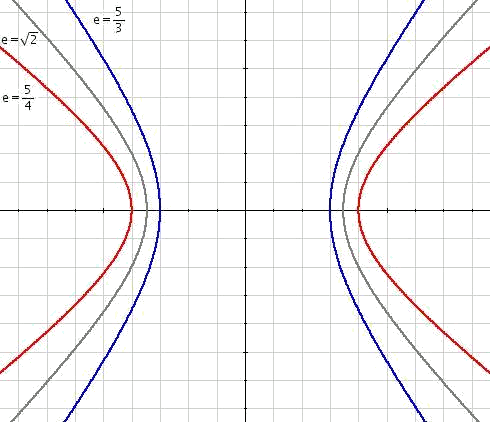
Una hipérbola es la curva formada por el conjunto de puntos del plano cuya diferencia de distancias a dos puntos fijos, los focos, es constante: $$\overline{PF}- \overline {PF'}=2a$$
- Focos: Son los dos puntos fijos $$F$$ y $$F'$$.
- Eje focal: Es el eje creado por la recta $$FF'$$ y cuya longitud es la distancia focal.
- Distancia focal o real: Distancia del segmento $$\overline{FF'}=2c$$.
- Eje secundario o imaginario: Eje formado por el conjunto de puntos equidistantes de $$F$$ y $$F'$$. Es por lo tanto la mediatriz del segmento $$\overline{FF'}$$.
- Centro: Es el punto medio del segmento $$\overline{FF'}$$. También es el punto donde se cruzan el eje focal y el eje secundario.
- Ejes de simetría: Tanto el eje focal como el eje secundario son ejes de simetría.
- Vértices: Los vértices $$A$$ y $$A'$$ son los puntos de intersección del eje focal con la hipérbola.
- Los vértices $$B$$ y $$B'$$ se obtienen de las intersecciones del eje secundario con el círculo de centro $$A$$ y de radio $$c$$.
- Por simetría también se hallan con el círculo de centro $$A'$$ y del mismo radio.
- Eje mayor: Es el eje creado por el segmento $$\overline{AA'}$$ y de longitud $$2a$$.
- Eje menor: Es el eje creado por el segmento $$\overline{BB'}$$ y de longitud $$2b$$.
- Relación entre semiejes: $$c^2=a^2+b^2$$.
- Radios vectores: Son los segmentos $$PF$$ y $$PF'$$, que unen los focos con un punto de la hipérbola.
- Asíntotas: Una hipérbola tiene dos asíntotas de ecuaciones respectivas $$\displaystyle y=\frac{b}{a}x$$ y $$\displaystyle y=-\frac{b}{a}x$$.
Excentricidad
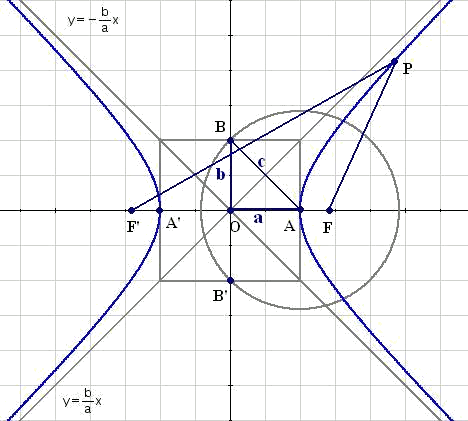
La excentricidad nos da informacion sobre la abertura de las ramas de la hipérbola. $$$\displaystyle e=\frac{c}{a}$$$ Como $$c\geq a$$, dividiendo a ambos lados por $$a$$: $$\displaystyle \frac{c}{a} \geq 1$$.
Se identifica entonces la excentricidad $$e \geq 1$$.
En el caso límite $$e=1$$ las ramas son horizontales. A medida que la excentricidad aumenta cada vez son más verticales las ramas de la hipérbola como se ve con $$\displaystyle e=\frac{5}{4}, e=\sqrt{2}$$ (hipérbola equilátera) y $$\displaystyle e=\frac{5}{3}$$.