Dos rectas en el plano pueden ser secantes, paralelas o coincidentes.
El siguiente dibujo muestra las 3 posibles situaciones:
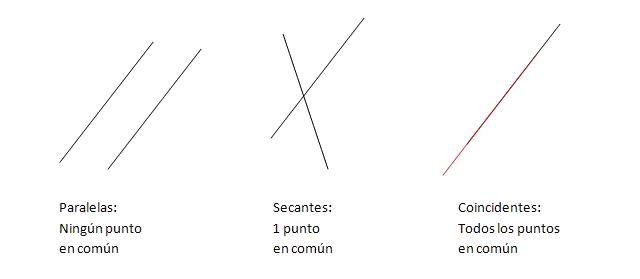
Veamos cómo distinguir entre los tres casos. Es necesario comentar que existen múltiples maneras de hacerlo dependiendo de la ecuación de la recta que tengamos. Evidentemente todas ellas serán equivalentes y si sabemos cómo pasar de una ecuación de la recta a otra, cualquier método de los siguientes nos servirá.
Veamos una forma geométrica de abordar el problema y una forma algebraica.
Desde un punto de vista geométrico, si consideramos dos rectas coincidentes como un caso particular de paralelismo, tenemos que dos rectas en el plano pueden ser únicamente paralelas o secantes.
¿Cuándo dos rectas son paralelas?
Cuando sus vectores directores son paralelos.
¿Cuándo dos vectores son paralelos?
Cuando uno es proporcional al otro. Esto es, si tenemos los vectores $$\overrightarrow{u}$$ y $$\overrightarrow{v}$$, deben de ser tales que $$\overrightarrow{u}=k\cdot\overrightarrow{v}$$ donde $$k$$ puede ser un número real cualquiera.
En coordenadas, si $$\overrightarrow{u}=(u_1,u_2)$$ y $$\overrightarrow{v}=(v_1,v_2)$$ los vectores son proporcionales y por tanto paralelos si y solo si $$$\dfrac{u_1}{v_1}=\dfrac{u_2}{v_2}$$$
Por tanto, ya tenemos una manera geométrica de encontrar la posición relativa de dos rectas, viendo si sus vectores directores son paralelos o no:
- Vectores directores paralelos:
- Si la rectas tienen un punto en común son coincidentes y son la misma.
- Si las rectas no tienen ningún punto en común son paralelas.
- Vectores directores no paralelos: las rectas son secantes.
Es importante notar que en general, dos rectas paralelas tienen vectores directores de componentes proporcionales y pendientes iguales.
Dadas las rectas $$r$$ y $$s$$, cuyas ecuaciones son respectivamente $$y=2x-7$$ y $$\dfrac{x-1}{3}=\dfrac{y-2}{5}$$, encontrad la posición relativa entre ellas y en caso que fueran secantes, el punto de corte:
De entrada buscamos vectores directores de ambas rectas.
Para $$y=2x-7$$ tenemos que la pendiente es $$m=2$$. Por tanto $$\overrightarrow{u}=(1, 2)$$ es un vector director de la recta $$r$$.
Para $$\dfrac{x-1}{3}=\dfrac{y-2}{5}$$ tenemos que $$\overrightarrow{v} = (3, 5)$$ es un vector director de la recta $$s$$.
Por tanto, si dividimos componente a componente tenemos: $$$\dfrac{u_1}{v_1}=\dfrac{1}{3}\neq\dfrac{2}{5}=\dfrac{u_2}{v_2} $$$ y por tanto los vectores directores no son paralelos y las rectas son secantes.
Resolvemos el sistema de ecuaciones formado por las ecuaciones de ambas rectas para encontrar el punto de corte: $$$\left\{\begin{array}{c} y=2x-7 \\ \dfrac{x-1}{3}=\dfrac{y-2}{5} \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ \dfrac{x-1}{3}=\dfrac{2x-7-2}{5} \end{array}\right. \Leftrightarrow $$$ $$$\Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ 5x-5=6x-27 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=2x-7 \\ x=22 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} y=37 \\ x=22 \end{array}\right.$$$
Por tanto el punto de corte entre las dos rectas es $$P = (22, 37)$$
Desde un punto de vista más algebraico, podemos analizar la posición relativa de dos rectas $$r$$ y $$s$$, a partir del número de soluciones del sistema de dos ecuaciones que forman las expresiones de las rectas $$r$$ y $$s$$.
Por ejemplo, si consideramos dos rectas $$r$$ y $$s$$, y sus respectivas ecuaciones implícitas:
$$\left\{\begin{array}{l} r: \ ax+by+c=0 \\ s: \ a'x+b'y+c'=0 \end{array}\right.$$
Tenemos que el sistema de ecuaciones:
$$\left\{\begin{array}{l} ax+by+c=0 \\ a'x+b'y+c'=0 \end{array}\right.$$
tiene por solución los puntos de intersección entre las rectas $$r$$ y $$s$$. Por tanto,
-
Si el sistema no tiene solución, las rectas son paralelas.
-
Si el sistema tiene infinitas soluciones, las rectas son coincidentes.
- Si el sistema tiene 1 solución, las rectas son secantes.
Dados los siguientes pares de rectas, encontrad la posición relativa entre ellas.
a) $$\left\{\begin{array}{c} -x+y=-1 \\ 2x+3y+3=0 \end{array}\right.$$
Resolvemos el sistema de ecuaciones: $$$\left\{\begin{array}{c} -x+y=-1 \\ 2x+3y+3=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x+2y=-2 \\ 2x+3y=-3 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x+2y=-2 \\ &+ & \underline{ \ \ \ 2x+3y=-3} \\ & & \ \ \ 0 \ \ +5y=-5 \end{eqnarray}\right.$$$
Y la solución del sistema es $$x = 0, \ y =-1$$. El hecho que la solución sea única nos indica que las rectas son secantes y el punto de corte es la solución del sistema.
b) $$\left\{\begin{array}{c} x+2y=2 \\ 2x+4y+1=0 \end{array}\right.$$
Resolvemos el sistema de ecuaciones: $$$\left\{\begin{array}{c} x+2y=2 \\ 2x+4y+1=0 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x-4y=-4 \\ 2x+4y=-1 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x-4y=-4 \\ &+ & \underline{ \ \ \ 2x+4y=-1} \\ & & \ \ \ \ \ \ \ \ 0 \ \ \ \ \ =-5 \end{eqnarray}\right.$$$
Y como el sistema no tiene solución podemos concluir que las dos rectas son paralelas.
c) $$\left\{\begin{array}{c} -x+y=1 \\ 2x-2y=-2 \end{array}\right.$$
Resolvemos el sistema de ecuaciones: $$$\left\{\begin{array}{c} -x+y=1 \\ 2x-2y=-2 \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} -2x+2y=2 \\ 2x-2y=-2 \end{array}\right. \Leftrightarrow \left\{\begin{eqnarray} & & -2x+2y=2 \\ &+ & \underline{ \ \ \ 2x-2y=-2} \\ & & \ \ \ \ \ \ \ \ 0 \ \ \ \ \ =0 \end{eqnarray}\right.$$$
Y como el sistema tiene infinitas soluciones, las dos rectas han de ser coincidentes.
