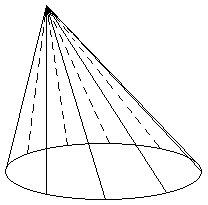
Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos. Los elementos notables del cono son:
-
El eje es el cateto fijo alrededor del cual gira el triángulo.
-
La base es el círculo engendrado por el otro cateto.
-
La generatriz es la hipotenusa del triángulo rectángulo.
- La altura es la distancia entre el vértice y la base.
Tronco de cono: es el cuerpo geométrico que resulta al cortar un cono por un plano paralelo a la base y separar la parte que contiene el vértice. La sección determinada por el corte es la base menor.
Cálculo de la generatriz
-
Generatriz del cono:
El cono es un cuerpo de revolución engendrado por un triángulo rectángulo al girar en torno a uno de sus catetos, que será la altura del cono y la hipotenusa será la generatriz. Por el teorema de Pitágoras la generatriz del cono será igual a: $$$ g=\sqrt{h^2+r^2}$$$
-
Generatriz del tronco de cono:
El tronco de cono es un cuerpo de revolución engendrado por un trapecio rectángulo al girar en torno al lado perpendicular a las bases, que será la altura del cono y el otro lado será la generatriz. Obtenemos la generatriz del tronco de cono aplicando el teorema de Pitágoras en el triángulo sombreado: $$$ g=\sqrt{h^2+(R-r)^2} $$$
Clasificación de los conos
-
El cono recto es el que su vértice equidista de la base circular.
-
El cono oblicuo es el que su vértice no equidista de su base.