Comparació dels infinits

En quan sabem que una funció pot tendir a infinit ens plantegem el fet que algunes funcions tendeixen a infinit molt més ràpid que altres i per tant, un infinit pot ser major que un altre no per ser més gran sinó per ser assolit abans per la funció.

Un bon exemple pot ser el següent:

Prenguem les funcions $f(x)=e^x$ i $g(x)=\ln x$.

Si les representem gràficament observarem que la funció exponencial creix molt ràpid mentre que la funció logaritme té un creixement molt lent. Les dues arriben a l'infinit, però la funció exponencial arriba a l'infinit molt més ràpid que la logarítmica, de manera que diem que l'infinit de la funció exponencial és més gran que el del logaritme.

Funció exponencial:

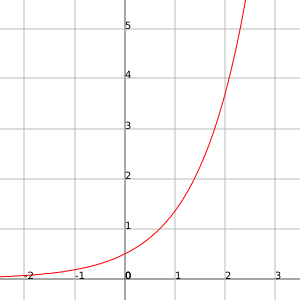
Funció logaritme:

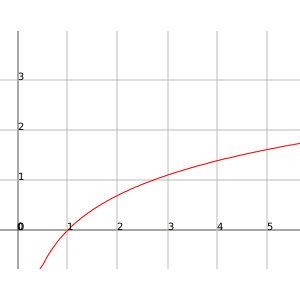
Llavors, com distingim si una funció tendeix a infinit més ràpidament que una altra funció?

Aquesta qüestió es resol utilitzant la divisió de funcions:

Suposem que ${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}f(x)=\pm \mathrm{\infty }}$ i que ${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}g(x)=\pm \mathrm{\infty }}$.

Diem que l'infinit de $f(x)$ és un infinit d'ordre superior al de $g(x)$ si:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{f(x)}{g(x)}=\pm \mathrm{\infty }}$$

o equivalentment si:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{g(x)}{f(x)}=0}$$

En cas que:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{f(x)}{g(x)}=k}$$

on $k$ és un valor real, llavors diem que els infinits de les dues funcions són equivalents o del mateix tipus.

Vegem com es comporten les funcions potència, exponencial i logarítmica al respecte:

• Donades dues potències de $x$, la de major exponent té un infinit d'ordre superior, si:

$$n>k\Rightarrow {\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{x^n}{x^k}={\displaystyle \underset{x\to +\mathrm{\infty }}{lim}{x}^{n-k}=+\mathrm{\infty }}}$$

on $n$ i $k$ poden ser valors reals positius.

En cas de tenir el mateix exponent en les dues potències obtindrem que:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{a{x}^n}{b^n}={\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{a}{b}=\frac{a}{b}}}$$

Per tant, si tenim un límit de divisió de polinomis, com sabem que l'infinit major vindrà donat per la potència més gran, podrem calcular el límit fixant-nos només en quin dels dos polinomis està aquesta potència més gran.

Vegem alguns exemples més:

• Donades dues funcions exponencials de bases majors que $1$, la de major base serà un infinit d'ordre superior, si $a>b>0$ llavors:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{a^x}{b^x}=+\mathrm{\infty }}$$

Vegem alguns exemples:

A més, qualsevol funció exponencial de base més gran que $1$ és un infinit d'ordre superior a qualsevol potència: si $a>1$ i $n<0$ aleshores:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{a^x}{x^n}=+\mathrm{\infty }}$$

Vegem alguns exemples:

• Donades dues funcions logarítmiques de base més gran que $1$, els infinits corresponents són sempre equivalents (o del mateix ordre).

Això vol dir que si $a>1$ i $b>1$ aleshores:

$${\displaystyle \underset{x\to +\mathrm{\infty }}{lim}\frac{{\log }_{a}x}{{\log }_{b}x}=k}$$

on $k$ és un valor real.

A més, qualsevol funció potència és un infinit d'ordre superior a qualsevol funció logarítmica (i per tant qualsevol a una funció exponencial també).

• Acabem comentant que si en una suma hi ha diversos tipus de sumands infinits, l'ordre de la suma és el del sumant de major ordre: