En el preciso momento que sabemos que una función puede tender a infinito nos planteamos el hecho de que algunas funciones tienden a infinito mucho más rápido que otras y por lo tanto, un infinito puede ser mayor que otro no por ser más grande sino por ser alcanzado antes por la función.
Un claro ejemplo puede ser el siguiente:
Tomemos las funciones $$f(x)=e^x$$ y $$g(x)=\ln x$$.
Si las representamos gráficamente observaremos que la función exponencial crece muy rápido mientras que la función logaritmo tiene un crecimiento muy lento. Las dos alcanzan el infinito, pero la función exponencial alcanza el infinito mucho más rápido que la logarítmica, por lo que decimos que el infinito de la función exponencial es más grande que la del logaritmo.
Función exponencial:
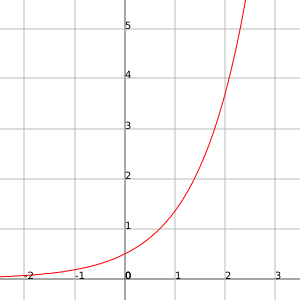
Función logaritmo:
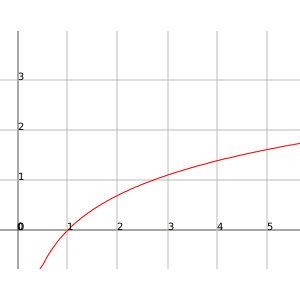
Entonces, ¿cómo distinguimos si una función tiende a infinito más rápidamente que otra función?
Esta cuestión se resuelve usando la división de funciones:
Supongamos que $$\displaystyle\lim_{x \to{+}\infty}{f(x)}= \pm \infty$$ y que $$\displaystyle\lim_{x \to{+}\infty}{g(x)}=\pm \infty$$.
Decimos que el infinito de $$f(x)$$ es un infinito de orden superior al de $$g(x)$$ si:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{f(x)}{g(x)}}= \pm \infty$$$
o equivalentemente si:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{g(x)}{f(x)}}=0$$$
En caso que:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{f(x)}{g(x)}=k}$$$
donde $$k$$ es un valor real, entonces decimos que los infinitos de las dos funciones son equivalentes o del mismo tipo.
Veamos como se comportan las funciones potencia, exponencial y logarítmica al respecto:
- Dadas dos potencias de $$x$$, la de mayor exponente tiene un infinito de orden superior, si:
$$$n>k \Rightarrow \displaystyle\lim_{x \to{+}\infty}{\frac{x^n}{x^k}}=\displaystyle\lim_{x \to{+}\infty}{x^{n-k}}=+\infty$$$
donde $$n$$ y $$k$$ pueden ser valores reales positivos.
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^5}{\sqrt[2]{x^5}}}=\displaystyle\lim_{x \to{+}\infty}{\frac{x^5}{x^{\frac{5}{2}}}}=\displaystyle\lim_{x \to{+}\infty}{x^{\frac{5}{2}}}=+\infty$$$
En caso de tener el mismo exponente en las dos potencias obtendremos que:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{ax^n}{b^n}}=\displaystyle\lim_{x \to{+}\infty}{\frac{a}{b}}=\frac{a}{b}$$$
Por lo tanto, si tenemos un límite de división de polinomios, como sabemos que el infinito mayor vendrá dado por la potencia más grande, podremos calcular el límite fijándonos solamente en cuál de los dos polinomios está esta potencia mayor.
Veamos algunos ejemplos:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{2x^3+2x^2-x+1}{x^4+44x^3-320x^2+x+3}}=\displaystyle\lim_{x \to{+}\infty}{\frac{2x^3}{x^4}}=\displaystyle\lim_{x \to{+}\infty}{\frac{2}{x}}=0$$$
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^2+3x^3-x+1}{x+3x^2+6x^3}}=\displaystyle\lim_{x \to{+}\infty}{\frac{3x^3}{6x^3}}=\frac{3}{6}=\frac{1}{2}$$$
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^3-x^4}{x^2+x}}\displaystyle\lim_{x \to{+}\infty}{\frac{-x^4}{x^2}}=-\infty$$$
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^3+2x-1}{x^2}}=\displaystyle\lim_{x \to{+}\infty}{\frac{x^3}{x^2}}=-\infty$$$
- Dadas dos funciones exponenciales de bases mayores que $$1$$, la de mayor base será un infinito de orden superior, si $$a>b>0$$ entonces:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{a^x}{b^x}}=+\infty$$$
Veamos algunos ejemplos:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{2^x}{1000 \cdot 1,5^x}}=+\infty$$$
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{2^x+e^x-4^x}{2^x-4,01^x}}=0$$$
Además, cualquier función exponencial de base mayor que $$1$$ es un infinito de orden superior a cualquier potencia, si $$a>1$$ y $$n<0$$ entonces:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{a^x}{x^n}}=+ \infty$$$
Veamos algunos ejemplos:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^{200}}{1,01^x}}=0$$$
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{x^2+3^x}{x^3+2^x}}=+\infty$$$
- Dadas dos funciones logarítmicas de base mayor que $$1$$, los infinitos correspondientes son siempre equivalentes (o del mismo orden).
Esto significa que si $$a>1$$ y $$b>1$$ entonces:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{\log_{a} x}{\log_{b}x}}=k$$$
donde $$k$$ es un valor real.
Además, cualquier función potencia es un infinito de orden superior a cualquier función logarítmica (y por consiguiente a cualquier función exponencial también).
- Acabamos comentando que si en una suma hay varios tipos de sumandos infinitos, el orden de la suma es el del sumando de mayor orden:
$$$\displaystyle\lim_{x \to{+}\infty}{\frac{2+2x-2^x+\log_{2}x+x^2}{\log_{4}x+4+4^x+4x}}=\displaystyle\lim_{x \to{+}\infty}{\frac{-2^x}{4^x}}=0$$$
