Límites finitos
Empezaremos mostrando un pequeño resumen de las propiedades de los límites finitos.
Supongamos que $$\displaystyle\lim_{x \to \pm \infty}{f(x)}=a$$ y que $$\displaystyle\lim_{x \to \pm \infty}{g(x)}=b$$, entonces se cumple que:
- $$\displaystyle\lim_{x \to \pm \infty}{f(x) \pm g(x)}=\displaystyle\lim_{x \to \pm \infty}{f(x)} \pm \displaystyle\lim_{x \to \pm \infty}{g(x)}=a \pm b$$
- $$\displaystyle\lim_{x \to \cdot \infty}{f(x) \pm g(x)}=\displaystyle\lim_{x \to \pm \infty}{f(x)} \cdot \displaystyle\lim_{x \to \pm \infty}{g(x)}=a \cdot b$$
- Si $$b \neq 0$$, $$\displaystyle\lim_{x \to \cdot \infty}{\frac{f(x)}{g(x)}}=\frac{\displaystyle\lim_{x \to \pm \infty}{f(x)}}{\displaystyle\lim_{x \to \pm \infty}{g(x)}}=\frac{a}{b}$$
- Si $$f(x)>$$, $$\displaystyle\lim_{x \to \pm \infty}{f(x)^{g(x)}}=\displaystyle\lim_{x \to \pm \infty}{f(x)^{\displaystyle\lim_{x \to \pm \infty}{g(x)}}}=a^b$$
- Si $$n$$ impar o $$n$$ par y $$f(x)\geqslant0 \Rightarrow \displaystyle\lim_{x \to \pm \infty}{\sqrt[n]{f(x)}}=\sqrt[n]{\displaystyle\lim_{x \to \pm \infty}{f(x)}}=\sqrt[n]{a}$$
- Si $$\alpha >0$$ y $$f(x)>0$$, $$\displaystyle\lim_{x \to \pm \infty}{ \log_{\alpha}f(x)}=\log_{\alpha}\Big(\displaystyle\lim_{x \to \pm \infty}{f(x)}\Big)=\log_{\alpha}a$$
Si$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=3$$ y $$\displaystyle\lim_{x \to {+} \infty}{g(x)}=-5$$ entonces:
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)+g(x)}=3-5=-2$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)-g(x)}=3-(-5)=8$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x) \cdot g(x)}=3 \cdot (-5)=-15$$
- $$\displaystyle\lim_{x \to {+} \infty}{f(x)^g(x)}=3^{-5}=\frac{1}{3^5}=\frac{1}{243}$$
- $$\displaystyle\lim_{x \to {+} \infty}{g(x)^{f(x)}}$$ no existe porque $$g(x) < 0$$ para valores grnades de $$x$$.
- $$\displaystyle\lim_{x \to {+} \infty}{\sqrt[3]{g(x)}}=\sqrt[3]{-5}=-\sqrt[3]{5}$$
- $$\displaystyle\lim_{x \to {+} \infty}{\sqrt{g(x)}}$$ no existe porque $$g(x) < 0$$ para valores grnades de $$x$$.
Límites infinitos
Empecemos definiendo qué es un límite infinito de una función $$f(x)$$:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=+\infty \Longleftrightarrow \mbox{ dado un número arbitrario } k, \mbox{ existe otro número } h$$$
$$$\mbox{ tal que si } x>h \mbox{ entonces } f(x)>k$$$
Intuitivamente, nos viene a decir que podemos conseguir que $$f(x)$$ sea tan grande como queramos sólo escogiendo un valor suficientemente grande de $$x$$.
Análogamente se define:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)}=-\infty \Longleftrightarrow \mbox{ dado un número arbitrario } k, \mbox{ existe otro número } h$$$
$$$\mbox{ tal que si } x>h \mbox{ entonces } f(x)<-k$$$
y para límites donde $$x$$ tiende a menos infinito:
$$$\displaystyle\lim_{x \to {-} \infty}{f(x)}=+\infty \Longleftrightarrow \mbox{ dado un número arbitrario } k, \mbox{ existe otro número } h $$$
$$$\mbox{ tal que si } x<-h \mbox{ entonces } f(x)>k$$$
$$$\displaystyle\lim_{x \to {-} \infty}{f(x)}=-\infty \Longleftrightarrow \mbox{ dado un número arbitrario } k, \mbox{ existe otro número } h$$$
$$$\mbox{ tal que si } x<-h \mbox{ entonces } f(x)<-k$$$
Veamos tres ejemplos básicos de funciones que tienden a infinito:
$$k$$ésima potencia: si $$k>0, \displaystyle\lim_{x \to {+}\infty}{x^k}=+\infty$$
y en particular $$\displaystyle\lim_{x \to {+}\infty}{p\cdot x^k}=sign(p) \cdot \infty$$, donde $$p$$ es un valor real distinto de cero.
De este punto, deducimos que las funciones polinómicas tienden a infinito conforme $$x$$ se hace grande.
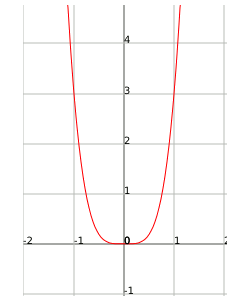
En este ejemplo podemos ver la función $$f(x)=3x^4$$. Cuando $$x$$ se hace grande, la función crece al infinito.
Exponenciales: si $$a>1, \displaystyle\lim_{x \to {+}\infty}{a^x}=+\infty$$
y de la misma manera si $$a>1, \displaystyle\lim_{x \to {+}\infty}{p \cdot a^x}=sign(p) \cdot \infty$$ .
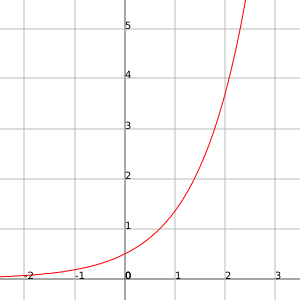
Un ejemplo para este caso es la función $$f(x)=\dfrac{1}{2}e^x$$. Tiende a infinito cuando $$x$$ tiende a infinito.
Logarítmicas: si $$a>1, \displaystyle\lim_{x \to {+}\infty}{\log_{a}x}=+ \infty$$
Análogamente, si $$a>1 \displaystyle\lim_{x \to {+}\infty}{\log_{a}x}=sign(p) \cdot \infty$$.
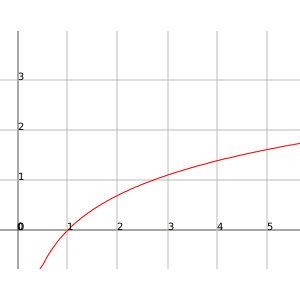
Por ejemplo, la función $$f(x)= \log_{e}x=\ln x$$. Esta función tiende al infinito cuando $$x$$ se hace grande muy lentamente.
Aritmética del infinito
Supongamos que $$\displaystyle\lim_{x \to {+} \infty}{f(x)}=+\infty$$ y que $$\displaystyle\lim_{x \to {+} \infty}{g(x)}=+\infty$$, entonces observamos sin problemas que se cumplirá que:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)+g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)}+\displaystyle\lim_{x \to {+} \infty}{g(x)}=+\infty + \infty=+\infty$$$
$$$\displaystyle\lim_{x \to {+} \infty}{f(x) \cdot g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)} \cdot \displaystyle\lim_{x \to {+} \infty}{g(x)}=(+\infty) \cdot (+\infty)=+\infty$$$
De todas formas, tendremos problemas cuando nos encontremos con situaciones como la siguiente:
$$$\displaystyle\lim_{x \to {+} \infty}{f(x)-g(x)}=\displaystyle\lim_{x \to {+} \infty}{f(x)}-\displaystyle\lim_{x \to {+} \infty}{g(x)}=(+\infty)-(+\infty)$$$
ya que restar infinito menos infinito nos da una indeterminación.
De la misma manera, podríamos plantearnos las propiedades entre una función con límite infinito y una con límite finito.
Veamos pues, una pequeña tabla que nos mostrará cómo se debe operar el infinito con otros infinitos y con límites finitos:
| SUMAS | PRODUCTOS |
| $$(+\infty)+a=+\infty$$ | $$(+\infty)\cdot(+\infty)=+\infty$$ |
| $$(+\infty)+(+\infty)=+\infty$$ | $$(+\infty)\cdot(-\infty)=-\infty$$ |
| $$(-\infty)+a=-\infty$$ | $$(+\infty)\cdot a=sign(a) \cdot \infty$$ |
| $$(-\infty)+(-\infty)=-\infty$$ | $$(-\infty)\cdot a=-sign(a) \cdot \infty$$ |
| $$-(-\infty)=+\infty$$ | |
| DIVISIONES | POTENCIAS |
| $$\frac{a}{\pm \infty}=0$$ | $$(+\infty)^{+\infty}=+\infty$$ |
| $$\frac{a}{0}=\pm \infty$$ if $$a\neq 0$$ | $$(+\infty)^{-\infty}=0$$ |
| $$\frac{\pm \infty}{0}=\pm \infty$$ | si $$a$$ > $$0$$ $$$(+\infty)^a= + \infty$$$ |
| $$\frac{0}{\pm \infty}=0$$ | si $$a$$ < $$0$$ $$$(+\infty)^a=0$$$ |
| si $$a\neq 0$$ $$$a^0=1$$$ | |
| si $$a$$ > $$1$$ $$$a^{+\infty}=+\infty \\ a^{-\infty}=0$$$ | |
| si $$0$$ <$$a$$ < $$1$$ $$$a^{+\infty}=0 \\ a^{-\infty}=+ \infty$$$ |
Estas operaciones se pueden realizar después de encontrar los límites de las funciones implicadas.
No obstante las operaciones que no están en la tabla pueden producir indeterminaciones, por ejemplo, son indeterminaciones las siguientes expresiones:
$$$(+\infty)-(+\infty) \\ 0 \cdot (\pm \infty) \\ \frac{0}{0} \\ (+\infty)^0 \\ 1^{\pm \infty} \\ 0^0 \\ \frac{\pm \infty}{\pm \infty}$$$
