Finite and infinite limits

Finite limits

We will start by showing a small summary of the properties of finite limits.

Let's suppose that $lim_{x \to \pm \infty} f (x) = a$ and that $lim_{x \to \pm \infty} g (x) = b$ , then also:

$lim_{x \to \pm \infty} f (x) \pm g (x) = lim_{x \to \pm \infty} f (x) \pm lim_{x \to \pm \infty} g (x) = a \pm b$
$lim_{x \to \cdot \infty} f (x) \pm g (x) = lim_{x \to \pm \infty} f (x) \cdot lim_{x \to \pm \infty} g (x) = a \cdot b$
If $b \neq 0$ , $lim_{x \to \cdot \infty} \frac{f (x)}{g (x)} = \frac{lim_{x \to \pm \infty} f (x)}{lim_{x \to \pm \infty} g (x)} = \frac{a}{b}$
If $f (x) >$ , $lim_{x \to \pm \infty} f (x)^{g (x)} = lim_{x \to \pm \infty} f (x)^{lim_{x \to \pm \infty} g (x)} = a^{b}$
If $n$ odd or if $n$ even and $f (x) ⩾ 0 \Rightarrow lim_{x \to \pm \infty} \sqrt[n]{f (x)} = \sqrt[n]{lim_{x \to \pm \infty} f (x)} = \sqrt[n]{a}$
If $α > 0$ and $f (x) > 0$ , $lim_{x \to \pm \infty} \log_{α} f (x) = \log_{α} (lim_{x \to \pm \infty} f (x)) = \log_{α} a$

Example

If $lim_{x \to + \infty} f (x) = 3$ and $lim_{x \to + \infty} g (x) = - 5$ then:

$lim_{x \to + \infty} f (x) + g (x) = 3 - 5 = - 2$
$lim_{x \to + \infty} f (x) - g (x) = 3 - (- 5) = 8$
$lim_{x \to + \infty} f (x) \cdot g (x) = 3 \cdot (- 5) = - 15$
$lim_{x \to + \infty} f (x)^{g} (x) = 3^{- 5} = \frac{1}{3^{5}} = \frac{1}{243}$
$lim_{x \to + \infty} g (x)^{f (x)}$ does not exist since $g (x) < 0$ for $x$ large enough.
$lim_{x \to + \infty} \sqrt[3]{g (x)} = \sqrt[3]{- 5} = - \sqrt[3]{5}$
$lim_{x \to + \infty} \sqrt{g (x)}$ does not exist since $g (x) < 0$ for $x$ large enough.

Infinite limits

Let's start by defining what an infinite limit of a function is $f (x)$ :

$lim_{x \to + \infty} f (x) = + \infty ⟺ given any k, there exists another number h$

$such that if x > h then f (x) > k$

Intuitively, it means that we can have $f (x)$ as big as we want by choosing a sufficiently large $x$ .

Similarly, we define:

$lim_{x \to + \infty} f (x) = - \infty ⟺ given any k, there exists another number h$

$such that if x > h then f (x) < - k$

and for limits when $x$ goes to minus infinity:

$lim_{x \to - \infty} f (x) = + \infty ⟺ given any k, there exists a another number h$

$such that if x < - h then f (x) > k$

$lim_{x \to - \infty} f (x) = - \infty ⟺ given any k, there exists a another number h$

$such that if x < - h then f (x) < - k$

Let's see three basic examples of functions that tend to infinity:

Example

$k$ th power: if $k > 0, lim_{x \to + \infty} x^{k} = + \infty$

and in particular $lim_{x \to + \infty} p \cdot x^{k} = s i g n (p) \cdot \infty$ , where $p$ is a real value other zero.

From this point, we deduce that the polynomial functions tend to infinity as $x$ becomes larger.

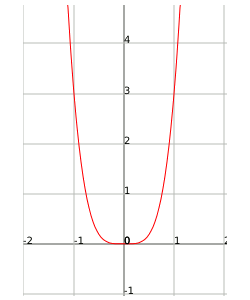
imagen

In this example we can see the function $f (x) = 3 x^{4}$ . When $x$ becomes large, the function grows to infinity.

Example

Exponential: if $a > 1, lim_{x \to + \infty} a^{x} = + \infty$

and likewise if $a > 1, lim_{x \to + \infty} p \cdot a^{x} = s i g n (p) \cdot \infty$ .

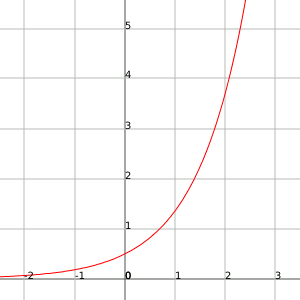
imagen

An example for this case is the function $f (x) = \frac{1}{2} e^{x}$ . It tends to infinity as $x$ tends to infinity.

Example

Logarithmic: if $a > 1, lim_{x \to + \infty} \log_{a} x = + \infty$

Similarly if $a > 1 lim_{x \to + \infty} \log_{a} x = s i g n (p) \cdot \infty$ .

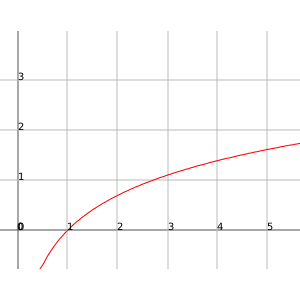
imagen

For example, the function $f (x) = \log_{e} x = \ln x$ . This function tends to infinity as $x$ becomes very large.

Infinite's arithmetic

Let's suppose that $lim_{x \to + \infty} f (x) = + \infty$ and that $lim_{x \to + \infty} g (x) = + \infty$ , then we observe without problems that:

$lim_{x \to + \infty} f (x) + g (x) = lim_{x \to + \infty} f (x) + lim_{x \to + \infty} g (x) = + \infty + \infty = + \infty$

$lim_{x \to + \infty} f (x) \cdot g (x) = lim_{x \to + \infty} f (x) \cdot lim_{x \to + \infty} g (x) = (+ \infty) \cdot (+ \infty) = + \infty$

However, we will have problems when we encounter situations like the following one:

$lim_{x \to + \infty} f (x) - g (x) = lim_{x \to + \infty} f (x) - lim_{x \to + \infty} g (x) = (+ \infty) - (+ \infty)$

since to if we subtract infinity from infinity it gives us an indeterminacy.

Similarly, we might ask ourselves about these properties when we a function with an infinite limit and one with a finite limit.

Let's see a small table that will show us how to work when we have different kinds necessary to produce infinity with other infinites and with finite limits:

SUMS	PRODUCTS
$(+ \infty) + a = + \infty$	$(+ \infty) \cdot (+ \infty) = + \infty$
$(+ \infty) + (+ \infty) = + \infty$	$(+ \infty) \cdot (- \infty) = - \infty$
$(- \infty) + a = - \infty$	$(+ \infty) \cdot a = s i g n (a) \cdot \infty$
$(- \infty) + (- \infty) = - \infty$	$(- \infty) \cdot a = - s i g n (a) \cdot \infty$
$- (- \infty) = + \infty$
DIVISIONS	POWERS
$\frac{a}{\pm \infty} = 0$	$(+ \infty)^{+ \infty} = + \infty$
$\frac{a}{0} = \pm \infty$ if $a \neq 0$	$(+ \infty)^{- \infty} = 0$
$\frac{\pm \infty}{0} = \pm \infty$	if $a$ > $0$ $(+ \infty)^{a} = + \infty$
$\frac{0}{\pm \infty} = 0$	if $a$ < $0$ $(+ \infty)^{a} = 0$
	if $a \neq 0$ $a^{0} = 1$
	if $a$ > $1$ $a^{+ \infty} = + \infty a^{- \infty} = 0$
	if $0$ < $a$ < $1$ $a^{+ \infty} = 0 a^{- \infty} = + \infty$

These operations can be realized after finding the limits of the functions involved.

Nevertheless, the operations that are not in the table can produce indeterminacies, for example, the following expressions:

$(+ \infty) - (+ \infty) 0 \cdot (\pm \infty) \frac{0}{0} (+ \infty)^{0} 1^{\pm \infty} 0^{0} \frac{\pm \infty}{\pm \infty}$