Discontinuity of functions: Avoidable, Jump and Essential discontinuity

The functions that are not continuous can present different types of discontinuities.

First, however, we will define a discontinuous function as any function that does not satisfy the definition of continuity. In other words, if we can find a point of discontinuity we will say that the function is not continuous:

$f (x)$ is not continuous if exists $x = a$ belonging to $D o m (f)$ such that $lim_{x \to a^{\pm}} f (x) \neq f (a)$

Let's see an example of function that is not continuous:

Example

Let's take the function $f (x) = {\begin{array}{rcl} 1 & if & x \leq 0 \\ 2 & if & x > 0 \end{array}$ .

This function is not continuous since at the point $x = 0$ we observe that: $lim_{x \to 0^{+}} f (x) = lim_{x \to 0} 2 = 2 f (0) = 1$ and thus the side limit from the right does not coincide with the value of the function, we conclude that the function cannot be continuous. We can see the graphic representation next:

imagen

It is necessary to bear in mind that a discontinuity is defined on points at the domain of a function. If the function was not defined in a point, although it has behavior similar to that of a discontinuity it would not be a discontinous function, since that would not have satisfied the definition given here.

Avoidable discontinuity

An avoidable discontinuity in a point $x = a$ occurs when the side limits coincide, but the value of the function at this point is not, that is to say: $lim_{x \to a^{-}} f (x) = lim_{x \to a^{+}} = L f (a) \neq L$ It is reasonable that we call this type of discontinuity avoidable since the function in the discontinuity point seems continuous, but the point in particular does not satisfy the definition of continuity, so only by adding this point to the definition of the function, can we obtain a continuous function.

Let's see an example:

Example

Let's take the function ${\begin{array}{rcl} \frac{x^{2} - 4}{x + 2} & if & x \neq - 2 \\ 0 & if & x = - 2 \end{array}$

We can see quickly that at the point $x = - 2$ the function does not match correctly. Let's observe the continuity at this point: $\begin{array}{l} lim_{x \to - 2^{-}} f (x) = lim_{x \to - 2^{-}} \frac{x^{2} - 4}{x + 2} = lim_{x \to - 2^{-}} \frac{(x + 2) (x - 2)}{x + 2} = lim_{x \to - 2^{-}} x - 2 = - 4 \\ lim_{x \to - 2^{+}} f (x) = lim_{x \to - 2^{+}} \frac{x^{2} - 4}{x + 2} = lim_{x \to - 2^{+}} \frac{(x + 2) (x - 2)}{x + 2} = lim_{x \to - 2^{+}} x - 2 = - 4 \\ f (- 2) = 0 \end{array}$

Consequently, $f (x)$ has an avoidable discontinuity at the point $x = - 2$ .

Example

Let's take the function $f (x) = {\begin{array}{rcl} e^{x} & if & x < 0 \\ 0 & if & x = 0 \\ x + 1 & if & x > 0 \end{array}$

We observe quickly that the subfunctions that define our function are continuous. Therefore the function will be continuous if its subfunctions match correctly. It can be seen that we have problems at point $x = 0$ .

Let's see what happens exactly: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} e^{x} = e^{0} = 1 \\ lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} x + 1 = 0 + 1 = 1 \\ f (0) = 0 \end{array}$

Consequently, $f (x)$ has an avoidable discontinuity at the point $x = 0$ .

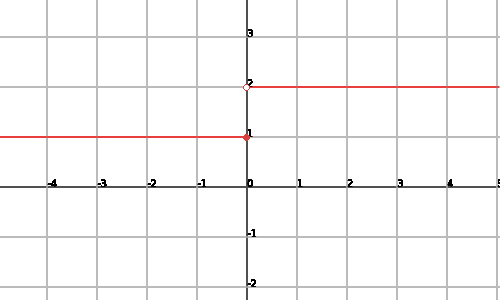
Jump discontinuity

A function $f (x)$ has an jump discontinuity at the point $x = a$ if the side limits of the function at this point do not coincide (and they are finite) that is: $\begin{array}{l} lim_{x \to a^{-}} f (x) \neq lim_{x \to a^{+}} f (x) \\ f (a) = L \end{array}$ independently of the value of the function at $x = a$ (of the value of $f (a)$ ).

If we denote this discontinuity with the name of "jump", it is also in contrast to the avoidable discontinuities. In this case we can not give the appropriate value to the discontinuity point since the side limits do not coincide. The following example will show clearly what we mean:

Example

Let's take the function $f (x) = {\begin{array}{rcl} x + 1 & if & x \leq 0 \\ x - 1 & if & x > 0 \end{array}$

we can see that in the zero we have: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0} x + 1 = 1 \\ lim_{x \to 0 +} f (x) = lim_{x \to 0} x - 1 = - 1 \\ f (0) = 1 \end{array}$ and since the limits do not coincide, we have an jump discontinuity (even though $f (0) = 1$ , which coincides with the limit from the left).

We can see the graphic representation of the function:

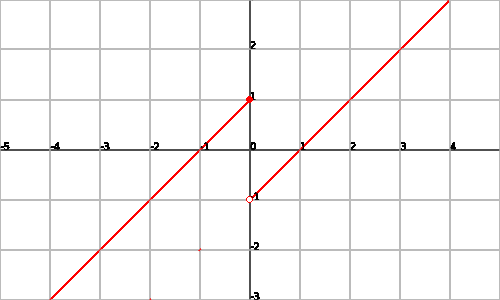
imagen

Example

Let's take the function $f (x) = {\begin{array}{rcl} e^{x} & if & x < 1 \\ x^{2} & if & x \geq 1 \end{array}$

The function will be continuous at the point $x = 1$ if the side limits and the function coincide. Let's see its behavior: $\begin{array}{l} lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} e^{x} = e \\ lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} x^{2} = 1 \\ f (1) = (1)^{2} = 1 \end{array}$

Consequently, we have an jump discontinuity.

Essential discontinuity

A function $f (x)$ has an essential discontinuity at point $x = a$ if some of the following cases are satisfied:

The side limits do not coincide.
Some of the side limits or both are infinity.

Let's see exactly every point:

We might be in the previous case, inevitable discontinuity.
But if we have : $lim_{x \to a^{-}} f (x) = \pm \infty$ and/or $lim_{x \to a^{+}} f (x) = \pm \infty$ and the function is defined in $x = a$ (independently of its value).

In these cases we say that we have a vertical asymptote. For more on this issue it may be worth looking at the unit on graphic representation.

Let's see an example:

Example

Let's take the function $f (x) = {\begin{array}{rcl} \frac{1}{x} & if x \neq 0 \\ 1 & if & x = 0 \end{array}$ we can see that at zero we have some problem of continuity, so we look at what happens with the continuity of the function at this point: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} \frac{1}{x} = \frac{1}{0^{-}} = - \infty \\ lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} \frac{1}{x} = \frac{1}{0 ⁺} = \infty \\ f (0) = 1 \end{array}$ Therefore we have an essential discontinuity at point $x = 0$ .

We can see a graphic representation of the function:

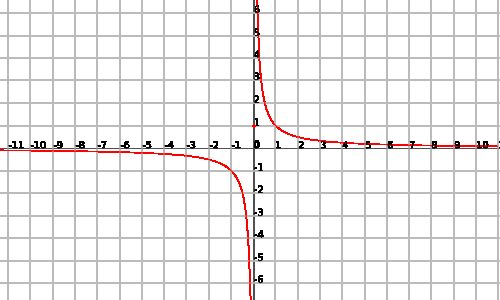
imagen

Attention! The function $f (x) = \frac{1}{x}$ does not present essential discontinuity since the function is continuous.

We would have the discontinuity at the point $x = 0$ , but it is not of the domian of the function, so it is not possible to define the discontinuity.

Nevertheless, the function has a vertical asymptote at $x = 0$ and has similar behavior to that of essential discontinuity.