Discontinuidad de funciones: evitable, inevitable (o de salto finito) y esencial

Las funciones que no son continuas pueden presentar diferentes tipos de discontinuidades.

Para empezar definiremos función no continua como aquella que no cumple la definición de función continua, es decir, existe algun punto del dominio donde el límite de la función a ese punto no es igual al valor de ésta en el mismo punto:

$f (x)$ no es continua si existe un $x = a$ perteneciente al $D o m (f)$ tal que $lim_{x \to a^{\pm}} f (x) \neq f (a)$

Veamos un ejemplo de función no continua:

Ejemplo

Tomemos la función $f (x) = {\begin{array}{rcl} 1 & si & x \leq 0 \\ 2 & si & x > 0 \end{array}$ .

Esta función no es continua ya que en el punto $x = 0$ observamos que: $lim_{x \to 0^{+}} f (x) = lim_{x \to 0} 2 = 2 f (0) = 1$ y como el límite lateral por la derecha no coincide con el valor de la función, deducimos que la función no puede ser continua. Podemos ver la representación gráfica a continuación:

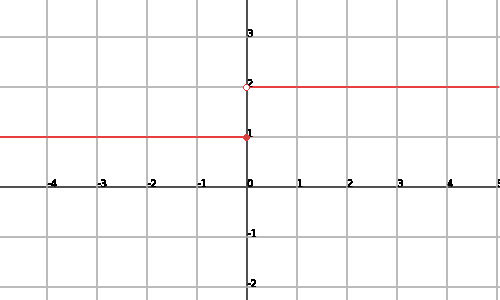
imagen

Se tiene que tener en cuenta que se define una discontinuidad sobre puntos del dominio de una función. Si la función no estubiese definida en un punto, aunque tenga comportamiento parecido al de una discontinuidad, no tendría ninguna, ya no se podría aplicar la definición de discontinuidad.

Discontinuidad evitable

Una discontinuidad evitable en un punto $x = a$ es aquella en que los límites laterales coinciden, pero el valor de la función en el punto no, es decir: $lim_{x \to a^{-}} f (x) = lim_{x \to a^{+}} = L f (a) \neq L$ Es razonable que llamen discontinuidad evitable a este tipo de discontinuidades ya que la función en el punto de discontinuidad parece que sea continua, pero el punto en concreto no existe, así que sólo añadiendo ese punto, lograríamos que la función fuera continua (se podría evitar la discontinuidad muy fácilmente).

Veamos un ejemplo:

Ejemplo

Tomemos la función ${\begin{array}{rcl} \frac{x^{2} - 4}{x + 2} & si & x \neq - 2 \\ 0 & si & x = - 2 \end{array}$

Podemos ver rápidamente que en el punto $x = - 2$ puede que la función no conecte correctamente. Observemos pues la continuidad en ese punto: $\begin{array}{l} lim_{x \to - 2^{-}} f (x) = lim_{x \to - 2^{-}} \frac{x^{2} - 4}{x + 2} = lim_{x \to - 2^{-}} \frac{(x + 2) (x - 2)}{x + 2} = lim_{x \to - 2^{-}} x - 2 = - 4 \\ lim_{x \to - 2^{+}} f (x) = lim_{x \to - 2^{+}} \frac{x^{2} - 4}{x + 2} = lim_{x \to - 2^{+}} \frac{(x + 2) (x - 2)}{x + 2} = lim_{x \to - 2^{+}} x - 2 = - 4 \\ f (- 2) = 0 \end{array}$

Por consiguiente, $f (x)$ tiene una discontinuidad evitable en el punto $x = - 2$ .

Ejemplo

Tomemos la función $f (x) = {\begin{array}{rcl} e^{x} & si & x < 0 \\ 0 & si & x = 0 \\ x + 1 & si & x > 0 \end{array}$

Observamos rápidamente que las subfunciones que definen nuestra función son continuas. Por lo que la función será continua si sus subfunciones conectan correctamente. Puede ser que tengamos problemas en el punto $x = 0$ .

Veamos qué ocurre exactamente: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} e^{x} = e^{0} = 1 \\ lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} x + 1 = 0 + 1 = 1 \\ f (0) = 0 \end{array}$

Por consiguiente, $f (x)$ tiene una discontinuidad evitable en el punto $x = 0$ .

Discontinuidad inevitable (o de salto finito)

Una función $f (x)$ tiene una discontinuidad inevitable en el punto $x = a$ si los límites laterales de la función en este punto no coinciden (y son finitos), es decir: $\begin{array}{l} lim_{x \to a^{-}} f (x) \neq lim_{x \to a^{+}} f (x) \\ f (a) = L \end{array}$ independientemente del valor de la función en $x = a$ (del valor de $f (a)$ ).

Si nos fijamos con el nombre de "inevitable", es razonable que se llame así ya que a diferencia de las discontinuidades evitables, esta vez al no ser iguales los límites laterales no hay manera de poder conectar las dos ramas de la función. Con un ejemplo veremos claramente lo que está pasando:

Ejemplo

Tomemos la función $f (x) = {\begin{array}{rcl} x + 1 & si & x \leq 0 \\ x - 1 & si & x > 0 \end{array}$

podemos ver que en el cero tenemos: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0} x + 1 = 1 \\ lim_{x \to 0 +} f (x) = lim_{x \to 0} x - 1 = - 1 \\ f (0) = 1 \end{array}$ y al no coincidir los límites, tenemos una discontinuidad inevitable (teniendo incluso que $f (0) = 1$ , que significa que tenemos continuidad lateral por la izquierda).

Podemos ver la representación gráfica de la función:

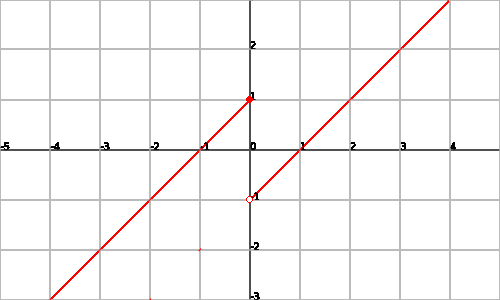
imagen

Ejemplo

Tomemos la función $f (x) = {\begin{array}{rcl} e^{x} & si & x < 1 \\ x^{2} & si & x \geq 1 \end{array}$

La función será continua si en el punto $x = 1$ los límites laterales y la función coinciden. Veamos su comportamiento: $\begin{array}{l} lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} e^{x} = e \\ lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} x^{2} = 1 \\ f (1) = (1)^{2} = 1 \end{array}$

Por consiguiente, tenemos una discontinuidad inevitable.

Discontinuidad esencial

Una función $f (x)$ tiene una discontinuidad esencial en el punto $x = a$ si se cumplen alguno de los siguientes casos:

Los límites laterales no coinciden.
Alguno de los límites laterales o ambos son infinitos.

Veamos pues exactamente cada caso:

Estamos en el caso anterior, discontinuidad inevitable.
Se cumple que : $lim_{x \to a^{-}} f (x) = \pm \infty$ y/o $lim_{x \to a^{+}} f (x) = \pm \infty$ y la función está definida en $x = a$ (independientemente de su valor).

En estos casos aparecen las asíntotas verticales. Para más sobre éstas consultar el tema de representación gráfica.

Veamos un ejemplo:

Ejemplo

Tomemos la función $f (x) = {\begin{array}{rcl} \frac{1}{x} & si x \neq 0 \\ 1 & si & x = 0 \end{array}$ podemos ver que el cero seguramente tendremos algun problema de continuidad, así que miremos qué pasa con la continuidad de la función en este punto: $\begin{array}{l} lim_{x \to 0^{-}} f (x) = lim_{x \to 0^{-}} \frac{1}{x} = \frac{1}{0^{-}} = - \infty \\ lim_{x \to 0^{+}} f (x) = lim_{x \to 0^{+}} \frac{1}{x} = \frac{1}{0 ⁺} = \infty \\ f (0) = 1 \end{array}$ Por lo tanto tenemos una discontinuidad esencial en el punto $x = 0$ .

Podemos ver una representación gráfica de la función:

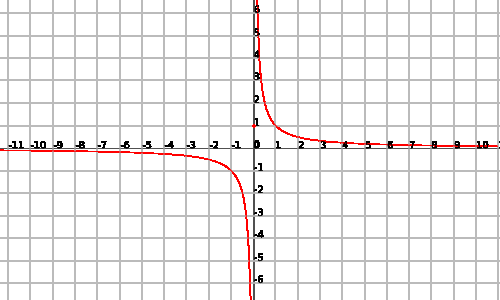
imagen

Atención! La función $f (x) = \frac{1}{x}$ no presenta discontinuidad esencial ya que la función es continua.

La discontinuidad la tendríamos en el punto $x = 0$ , pero éste no es del dominio de la función, así que no se puede definir la discontinuidad.

No obstante, la función sí tiene una asíntota vertical en $x = 0$ y tiene un comportamiento análogo al de la discontinuidad esencial.