Systems of inequations with two variables

As with the definition of system of inequations with one variable , we define the system of two variables:

A system of inequations with two variables is a set of inequations with two variables that act simultaneously; that is, the solution points must satisfy all the inequations of the system.

Example

An example of a system of inequations is: ${\begin{cases} y - x + 3 < 1 \\ y - x > x - 2 \end{cases}$

To look for the solution of the system, we will mainly use the definition of a system of two variables: we will look for the solutions of every inequation of the system and, next, we will look at where the regions of solution coincide.

Before looking for these regions, we must emphasize the fact that in the previous case, i.e., systems of inequations with one variable , it was much easier to intersect the inequations to find the common solution and, thereby, and find the solution of the system. In this case, the solutions of every inequation are regions in the plane, and it is possible that it is a little harder to find the common regions between all the regions of solution of every inequation of the system.

A possible method to find the common regions between all the inequations is to firstly find every region of every inequation and next draw all the solutions in the same plane. In this way, the regions will overlapp and it will be easier to see the regions of solution of the system.

Returning to the system of the example, let's find the solution to illustrate how it must be solved.

Example

First, we solve the inequations separately, obtaining in this way the respective solutions: ${\begin{cases} y < x - 2 \Rightarrow The solution region is which is below the straight line \\ y > 2 x - 2 \Rightarrow The solution region is which is above the straight line \end{cases}$

Next we can see both regions drawn in the plane:

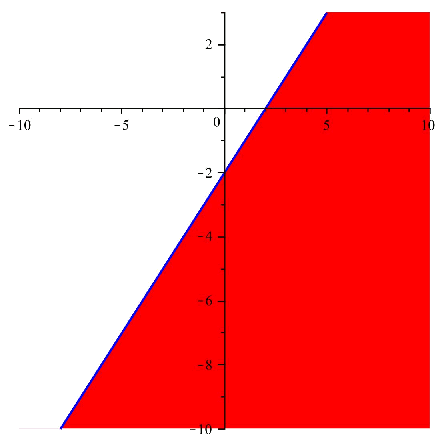
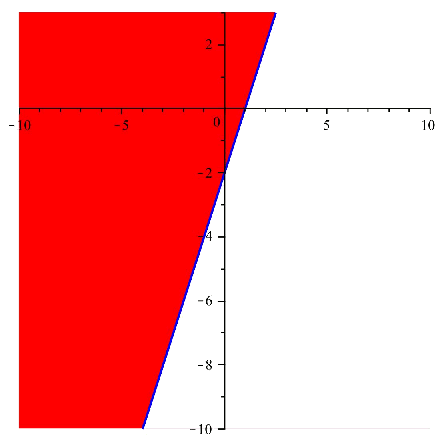
imagen imagen

And if we overlap the images, and we take the common region, we get:

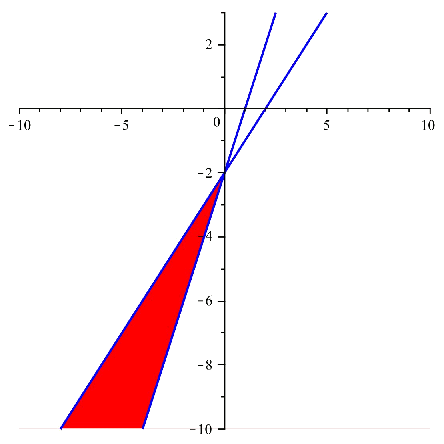
imagen

Solution region of the system:

This region can be written as ${\begin{cases} y < x - 2 \\ y > 2 x - 2 \end{cases}$ which equals the solution of each of the inequations.

To summarize, given a system of inequations, to solve it we have to solve every inequation separately and take the common region between all the regions of solution of every inequation.

Next, we show some examples of interesting cases of systems.

Example

${\begin{cases} y - x ⩽ 0 \\ x - y ⩽ 0 \end{cases}$

Resolution: ${\begin{cases} y - x ⩽ 0 \Rightarrow y ⩽ x \\ x - y ⩽ 0 \Rightarrow y ⩾ x \end{cases}$

Then, the common region is $y = x$ and we say that the solution is the line $y = x$ .

Example

${\begin{cases} 2 x - y > 2 \\ - 4 x + 2 > 1 \end{cases}$

Resolution: ${\begin{cases} 2 x - y > 2 \Rightarrow y < 2 x - 2 \\ - 4 x + 2 > 1 \Rightarrow y > 2 x + 1 \end{cases}$

Notice that the lines induced by the inequations are paralel and looking carefully we can see that the relation $2 x - 2 < 2 x + 1$ is true since $- 2 < 1$ and then it is fulfilled that $y < 2 x - 2 < 2 x + 1 < y$ and we will never find values $x$ and $y$ that can fulfill both inequations at the same time.

Then, it is impossible to solve the system.