Anàlogament a la definició de sistema d'inequacions d'una variable, definim la del sistema de dues variables:
Un sistema d'inequacions de dues variables és un conjunt d'inequacions de dues variables que actuen al mateix temps, és a dir, els punts solució han de complir totes les inequacions del sistema.
Un exemple de sistema d'inequacions és: $$$ \left\{ \begin{array}{l} y-x+3 < 1 \\ y-x > x-2 \end{array}\right. $$$
Per buscar la solució del sistema, farem ús principalment de la definició de sistema de dues variables: buscarem les solucions de cadascuna de les inequacions del sistema i després mirarem on coincideixen les regions solucions d'aquestes.
Abans de cercar aquestes regions, hem de recalcar el fet que en el cas anterior, sistemes d'inequacions d'una variable, era molt més senzill intersecar les inequacions per trobar la solució comú de totes i per tant la del sistema. En el cas d'ara les solucions de cada inequació són regions en el pla i pot ser que resulti una mica més complicat trobar les regions comunes entre totes les regions solucions de cada inequació del sistema.
Un possible mètode per trobar les regions comunes és trobar primer cada regió de cada inequació i a continuació dibuixar en un mateix pla totes les solucions juntes, solapant-se així les regions i podent veure fàcilment quines regions seran solució del sistema.
Tornant al sistema de l'exemple, anem a trobar la solució per mostrar com s'ha de fer.
Primer resolem les inequacions per separat, obtenint així les solucions respectives: $$$ \left\{ \begin{array}{l} y < x-2 \Rightarrow \text{ la regió solució és la que està sota la recta} \\ y > 2x-2 \Rightarrow \text{ la regió solució és la que està per sobre de la recta} \end{array}\right. $$$
A continuació podem veure aquestes dues regions dibuixades en el pla:
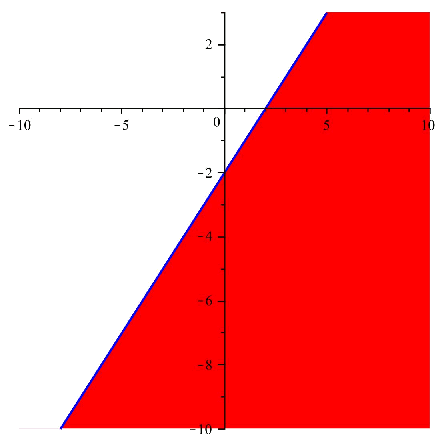
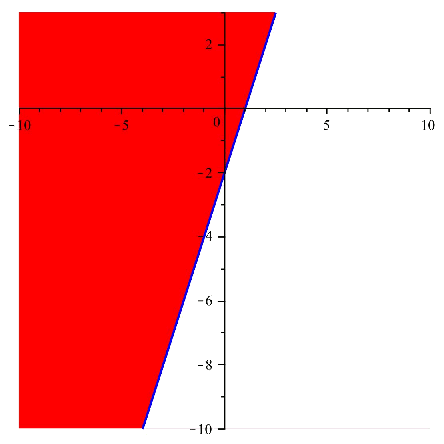
I si superposem les imatges, i prenem la regió comú, obtenim:
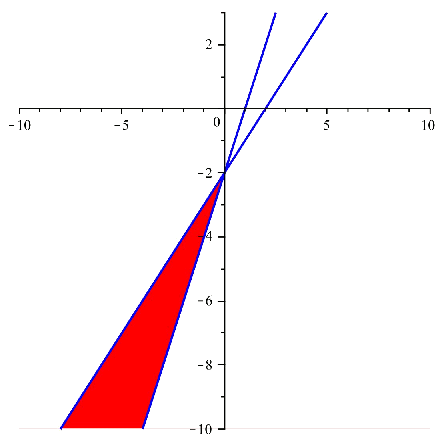
Regió solució del sistema:
Aquesta regió simplement es denota com $$$ \left\{ \begin{array}{l} y < x-2 \\ y > 2x-2 \end{array}\right. $$$ que justament és la solució de cadascuna de les inequacions.
En resum, donat un sistema d'inequacions, per resoldre'l només cal resoldre cadascuna de les inequacions per separat i prendre la regió comú d'entre totes les regions solució de cada inequació.
A continuació posem alguns exemples de casos interessants de sistemes.
$$$ \left\{ \begin{array}{l} y-x \leqslant 0 \\ x-y \leqslant 0 \end{array}\right. $$$
Resolució $$$ \left\{ \begin{array}{l} y-x \leqslant 0 \Rightarrow y\leqslant x \\ x-y \leqslant 0 \Rightarrow y\geqslant x \end{array}\right. $$$
En conseqüència la regió comú és $$y=x$$ i diem que la solució és la recta $$y=x$$.
$$$ \left\{ \begin{array}{l} 2x-y > 2 \\ -4x +2 > 1 \end{array}\right. $$$
Resolució $$$ \left\{ \begin{array}{l} 2x-y > 2 \Rightarrow y < 2x-2 \\ -4x +2 > 1 \Rightarrow y > 2x+1 \end{array}\right. $$$
Observem que les rectes induïdes per les inequacions són paral·leles i si ens fixem podem veure que la relació $$2x-2 < 2x+1$$ és certa ja que $$-2 < 1$$ i llavors es compleix $$ y < 2x-2 < 2x+1 < y$$ i per tant mai trobarem valors $$x$$ i $$y$$ que facin complir les dues inequacions a la vegada.
En conseqüència el sistema és impossible de resoldre.