¿Què és un triangle?

Un triangle és un polígon de tres costats determinat per tres segments de tres rectes que es tallen, anomenats costats. Els punts on es tallen aquests segments, i que evidentment mai estaran alineats, s'anomenen vèrtexs.
Elements bàsics del triangle
- Es diu altura a cadascuna de les perpendiculars traçades des d'un costat a vèrtex oposat.
- Les mediatrius d'un triangle són cadascuna de les perpendiculars dels seus costats des del seu punt mitjà.
- S'anomena mitjana d'un triangle a cada una de les rectes traçades des del punt mitjà d'un costat a vèrtex oposat.
- Les bisectrius són les rectes que divideixen per la meitat cada un dels vores del triangle.
Tipus de centres d'un triangle
Geomètricament es poden definir diversos centres en un triangle.
Baricentre
És el punt que es troba en la intersecció de les mitjanes, i equival al centre de gravetat.
Circumcentre
És el centre de la circumferència circumscrita, la que passa pels tres vèrtexs del triangle. Es troba a la intersecció de les mediatrius dels costats. A més, la circumferència circumscrita conté els punts d'intersecció de la mediatriu de cada costat amb les bisectrius que passen pel vèrtex oposat.
Incentre
És el centre de la circumferència inscrita, aquella que és tangent als costats del triangle. Es troba a la intersecció de les bisectrius dels rectangles.
Ortocentre
És el punt que es troba en la intersecció de les altures.
Exincentres
Són els centres de les circumferències exinscrites, aquelles que són tangents als costats del triangle. Es troba a la intersecció d'una bisectriu interior i dues bisectrius exteriors dels rectangles.
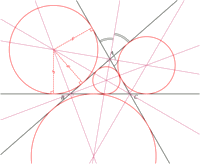
L'únic cas en què tots els centres coincideixen és el del triangle equilàter (tots els costats són iguals).
En concret, l'ortocentre, el baricentre i el circumcentre sempre estaran alineats i la recta que passa per ells s'anomena Recta d'Euler.





