Anem a aprendre a crear i resoldre un document del següent tipus:
Donat un conjunt de restriccions (inequacions), determinar la zona del pla en què es compleixen totes elles, donant els valors de les coordenades dels vèrtexs d'aquesta zona.
Normalment en els exercicis amb inequacions es té més d'una restricció simultàniament sobre les variables. Per exemple, si tenim com a problema el nombre de cadires (de
(i)
es tindran també les restriccions que tant el nombre de cadires (
(ii)
(iii)
Cadascuna d'aquestes restriccions té associada una recta en el pla XY, que separa el pla en dues regions: la regió de validesa (regió en què es compleix la restricció) i la zona en què no es compleix. A continuació es presenten aquestes rectes i zones de validesa per a les tres restriccions:
(i) La restricció és:
i per tant la recta associada és:
A més, si provem el punt
per tant la regió de validesa serà la que contingui el punt
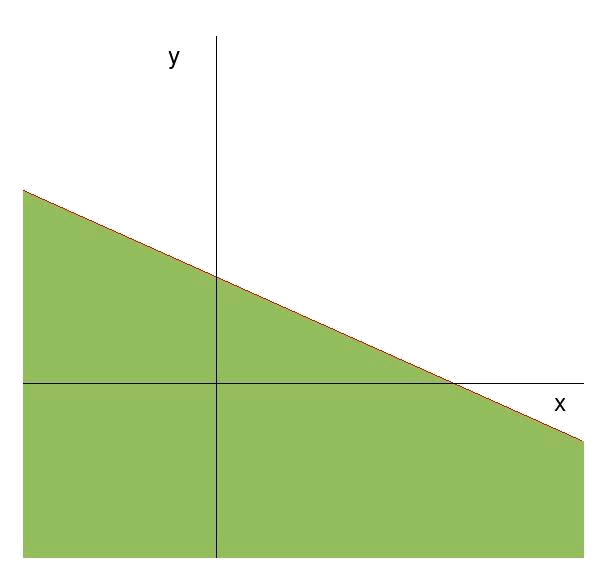
(ii) La restricció és:
Aquest tipus de restricció representa una recta vertical (paral.lela a l'eix
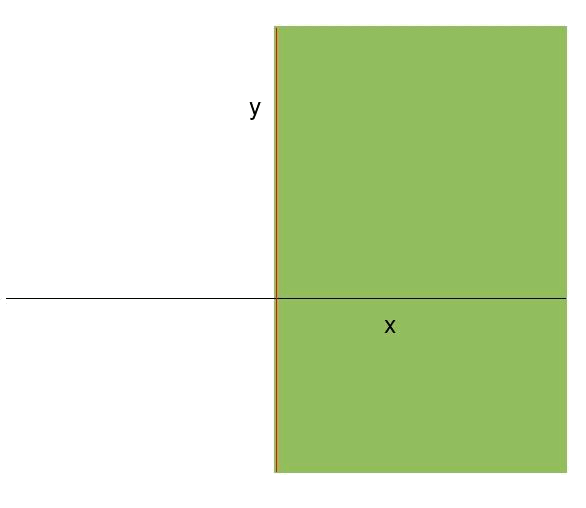
iii) La restricció és:
La recta associada a aquesta restricció és:
i la zona de validesa és, evidentment, la regió per sobre de

Ara seria qüestió de conèixer la regió del pla XY en què es compleixen totes les restriccions simultàniament. Aquesta regió serà la que sigui comuna a les regions de validesa de totes les restriccions. Per al cas de les cadires i les taules serà el triangle que formen la recta
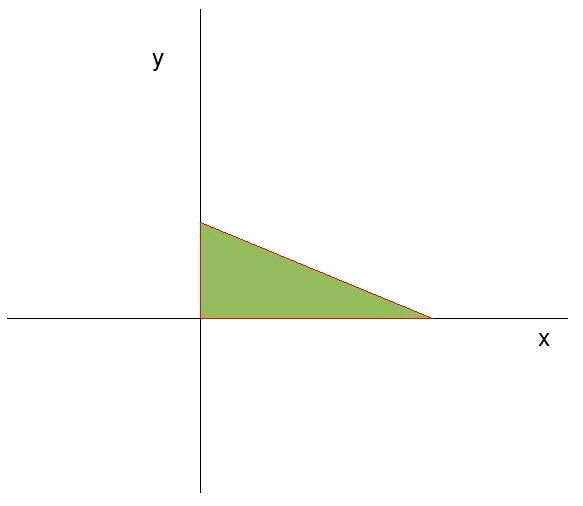
Veiem que en aquest cas, en tenir en compte totes les restriccions al mateix temps, la regió de validesa (a partir d'ara es referirà a la regió comú de totes les zones de validesa de les diferents restriccions com a regió de validesa a seques) és una zona acotada del pla. En els exemples anteriors la regió de validesa s'estenia per algun costat fins a l'infinit, per això no estaven delimitades aquestes zones.
Per conèixer bé la regió de validesa s'han de conèixer les coordenades dels seus vèrtexs. En aquest cas és molt senzill. Ja coneixem les coordenades d'un dels punts: el
Els punts de tall amb els eixos es poden trobar fàcilment:
-
Per al punt de tall amb l'eix
- El punt de tall amb l'eix
Així doncs els vèrtexs de la regió de validesa tenen per coordenades:
En aquest cas ha estat molt fàcil trobar els vèrtexs.
El següent exemple il·lustrarà la forma més general per trobar els vèrtexs de la regió de validesa.
Exemple
Es tenen les següents restriccions:
que tenen per rectes associades:
Podem visualitzar aquestes rectes i determinar els semiplans on es compleix cada inequació per separat.
Per a la recta
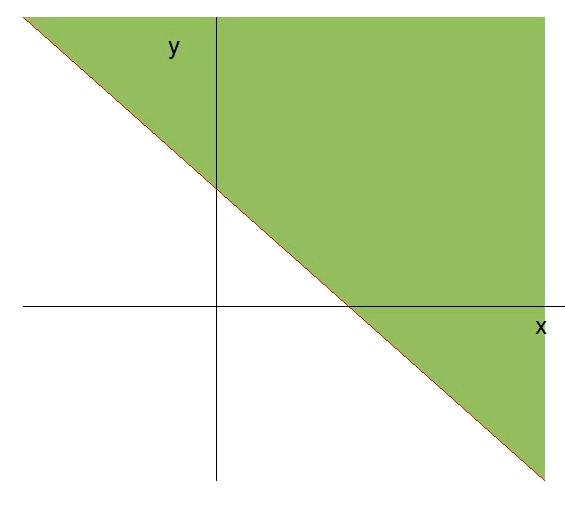
Com que no es compleix la inequació al punt
Per a la recta
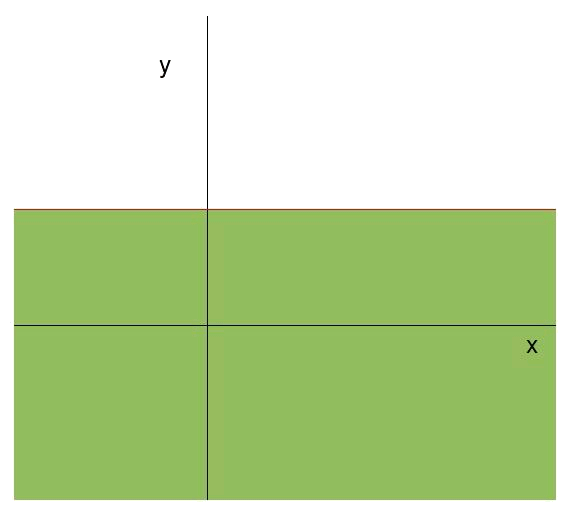
Com es compleix la inequació al punt
Per a la recta
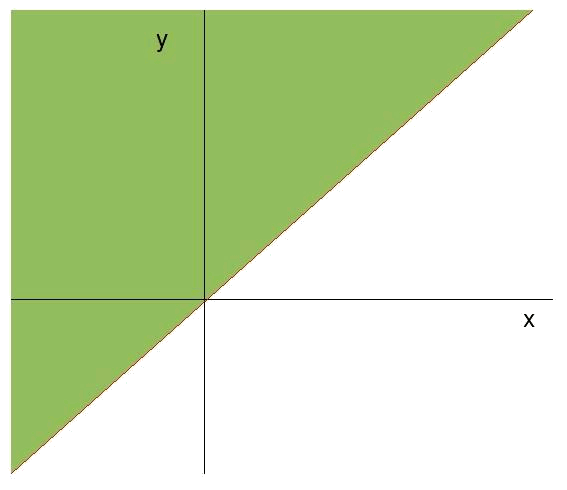
Com es compleix la inequació al punt
En conjunt tenim doncs:
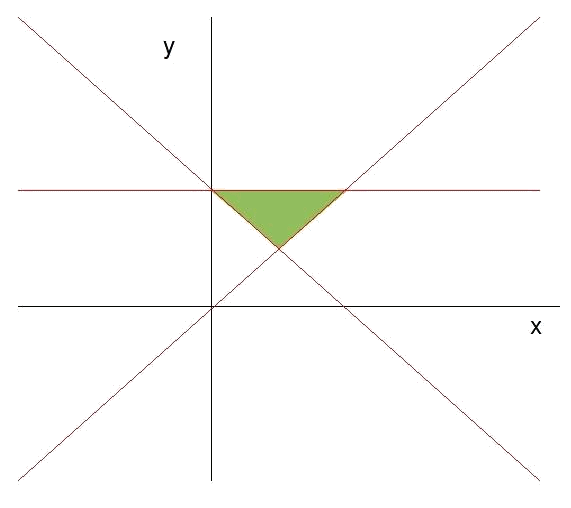
La zona on coincideixen tots els semiplans és la regió factible. Veiem que en aquest cas es tracta també d'una zona delimitada.
S'ha de realitzar ara el càlcul dels vèrtexs d'aquesta zona. Per a això es necessitarà saber el punt en què es tallen les rectes dos a dos. Haurem de trobar tres punts de tall: el de la recta
Com trobar el punt de tall de dues rectes:
Conèixer un punt significa saber les coordenades
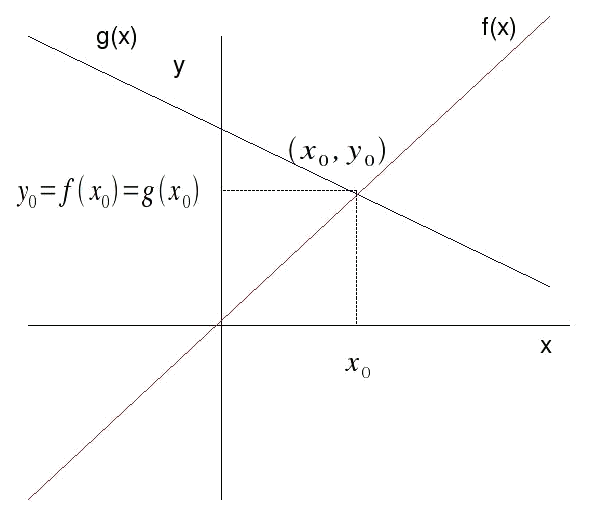
Per tant, sabem que el punt de tall serà
Exemple
Tornem a l'exemple.
Punt de tall entre
S'han de trobar les coordenades
Per trobar la coordenada
Per tant les dues rectes es tallen en
Determinar la coordenada
Per tant el punt de tall entre les rectes
Punt de tall entre
Es procedeix igual que en el cas anterior. Igualem les funcions
Com en el cas anterior, la coordenada
Així doncs, les coordenades del punt de tall són:
Punt de tall entre
Aquest punt de tall tindrà per coordenades
Es determina el valor de la coordenada
Per tant, el punt de tall entre les rectes
Així doncs els vèrtexs de la regió de validesa tenen per coordenades:
Altres exemples:
Exemple
Considerant el sistema d'inequacions següent:
Busquem primer les rectes associades a cada inequació i les zones de validesa de cadascuna:
- La primera d'elles ens dóna una recta paral.lela a l'eix
- La segona és una recta paral·lela a l'eix
- La tercera recta és
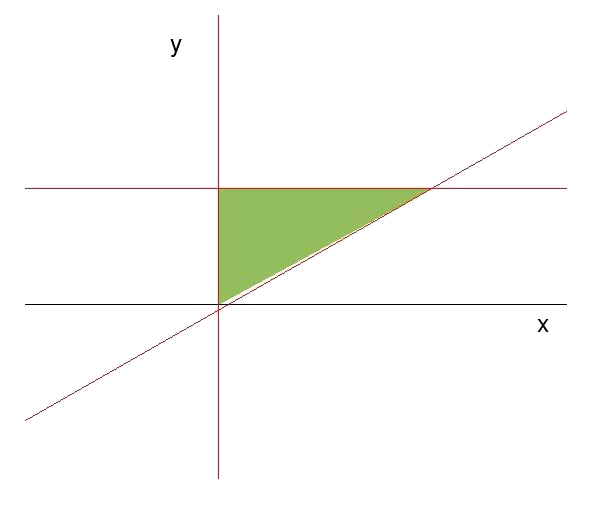
Determinarem els vèrtexs de la zona de validesa com els punts de tall entre les diferents rectes.
- La recta
- La recta
- La recta
Per tant, els vèrtexs de la regió de validesa són:
Exemple
Donat el conjunt de restriccions:
Busquem primer les rectes associades a cada restricció i les zones de validesa de cada inequació (comprovant amb un punt en les inequacions). Les rectes associades són:
Dibuixant les rectes i les zones de validesa podem visualitzar la regió de validesa.
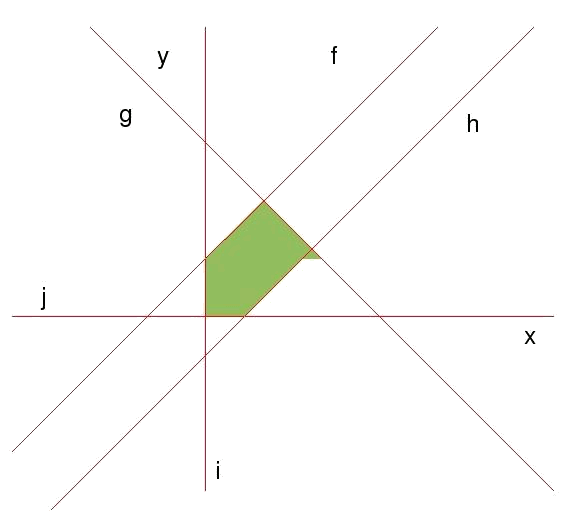
Si no podem fer el dibuix tenim una alternativa. Havent-hi tantes rectes, normalment es tindran més punts de tall entre les rectes, que vèrtexs a la zona de validesa. Per aquest motiu, no tots els punts de tall entre les diferents rectes seran vèrtexs de la regió de validesa. Per reconèixer quins són els vèrtexs de la regió de validesa es farà el següent:
-
Es calculen tots els punts de tall entre les diferents rectes.
- Aquells punts de tall en què es compleixin a la vegada totes les restriccions seran els vèrtexs de la zona de validesa (i així podrem dibuixar-la, si no ho hem fet abans).
Procedint d'aquesta manera amb el problema, anem a calcular tots els punts de tall entre les diferents rectes:
-
-
-
-
-
-
-
-
-
Determinació dels vèrtexs de la zona de validesa:
Es tenen nou punts de tall entre les rectes. Com s'ha dit abans, s'ha de comprovar en quins punts es compleixen totes les inequacions, i aquests seran els vèrtexs de la regió de validesa.
Per tant els vèrtexs de la regió de validesa són:
En resum, si es tenen diverses inequacions simultàniament, cadascuna determinarà un semiplà on es compleix. La intersecció d'aquests semiplans (regió conjunta a tots ells) se li dirà regió factible, i és la regió en què es compleixen totes les inequacions alhora. Aquesta zona pot estar acotada o no.
Es determinen els vèrtexs de la zona de validesa, determinant els punts de tall de les rectes de dos en dos. Si es tenen les dues rectes:
El punt de tall serà
La solució a aquesta equació és:
I les funcions
Essent doncs el punt de tall entre les dues rectes:
Així es calculen els vèrtexs de la regió de validesa o regió factible.
