In this section we will explain how to solve the following type of problems:
Given several restrictions (inequations), we have to determine the area on the plane that satisfies all of them by giving its vertexes.
We usually find more than one simultaneous restriction for the variables in inequations exercises. For example, if we have to find the number of chairs (of
(i)
but also restrictions of being positive both the number of chairs (
(ii)
(iii)
Each of these restrictions has a straight line associated with the plane XY, that separates the plane in two regions: the validity region (region where the restriction is satisfied) and the area in where it is not satisfied. Next for these straight lines and areas of validity, there are three restrictions:
(i) The restriction is:
and therefore the associated straight line is:
If we also try the point
therefore the validity region will be the one that contains the point
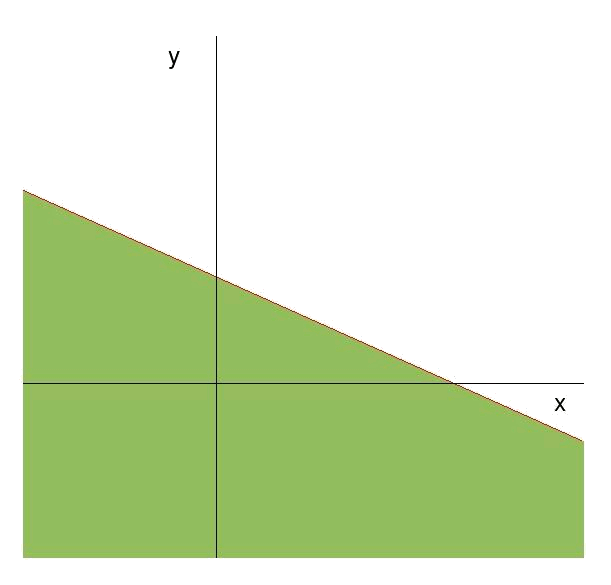
(ii) The restriction is:
This type of restriction represent a vertical straight line (parallel to the axis
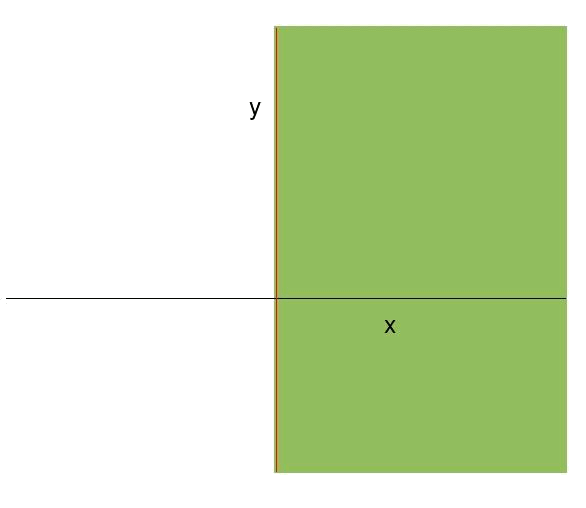
iii) The restriction is:
The straight line associated with this restriction is:
and the validity area is, obviously, the region over

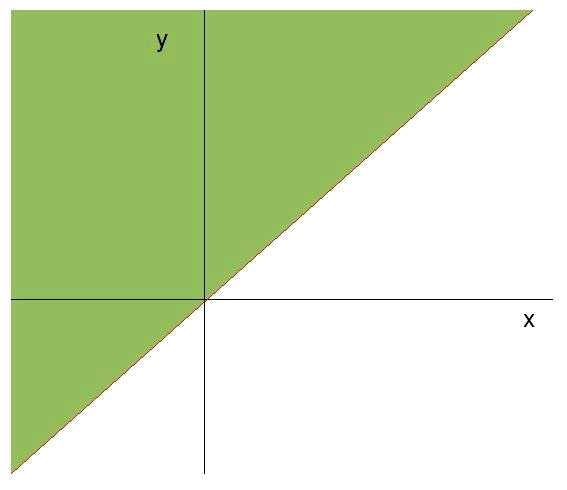
Now we should know the region of the plane XY where all the restrictions are satisfied simultaneously. This region will the one that is common to the validity regions that are free of restrictions. For the case of the chairs and the tables it will be the triangle composed by the straight line

We can see that in this case, as we take into account all the restrictions simultaneously, the validity region (from now on we will refer to the common region of all the areas of validity from the different restrictions simply as the validity region) is an enclosed area of the plane. In the previous examples the validity region was spreading over some side up to infinity, that's why these areas were not bounded.
To know the validity region well the coordinates of its apexes have to be known. In this case it is very simple. We already know the coordinates of one of the points:
The intersection points with the axes can be found easily:
-
For the cross point with the axis
- And the intersection point with the axis
So the apexes of the region of validity have as their coordinates:
In this case it has been very easy to find the apexes.
The following example will illustrate the most general way to find the apexes of the region of validity.
Example
We have the following restrictions:
that they take as associated straight lines:
We can visualize these straight lines and determine the semiplanes where every inequation is satisfied separately.
For the straight line

Since the inequation is not satisfied at point
For the straight line

Since the inequation is satisifed at point
For the straight line
Since the inequation is satisifed at point
As a whole we have:
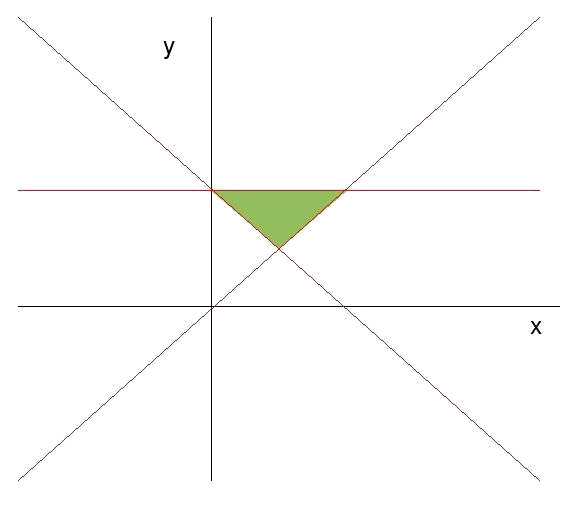
The area where all the semiplanes coincide is the feasible region. We see that in this case it is also a question of a bounded area.
Now the calculation of the apexes of this area has to be done. To do so, it will be necessary to know the point where the straight lines cross. We will have to find three intersection points: the one of the straight line
How to find the point of intersection of two straight lines:
To know a point means to know the coordinates
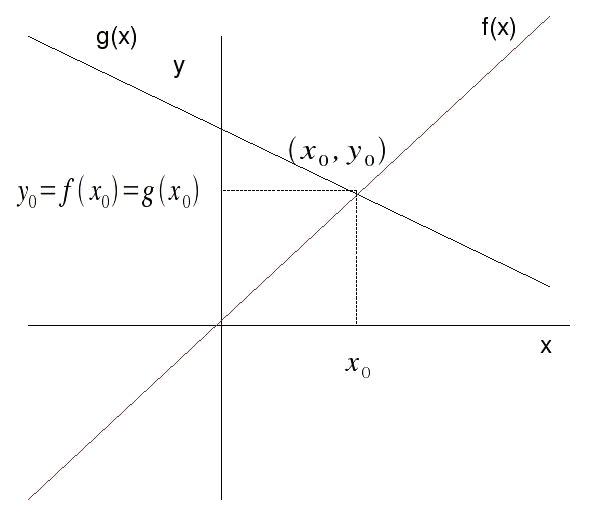
Therefore we know that the intersection point will be
Example
Back to the example.
Intersection point between
We have to find the coordinates
To find the coordinate
Therefore two straight lines cross at
Determining the coordinate
Therefore the intersection point between the straight lines
Intersection point between
We proceed just as in the previous case. We equal the functions
As in the previous case, the coordinate
And so, the coordinates of the point of intersection are:
Intersection point between
This intersection point will have as its coordinates
We decide the value of the coordinate
Therefore the intersection point between the straight lines
In short, the coordinates of the apexes of the feasible region are:
Other examples:
Example
Considering the following inequations system:
We look first for the straight lines associated with every inequation and the areas of validity of each one:
- The first of them gives us a straight line parallel to the axis
- The second one is a straight line parallel to the axis
- The third straight line is

We will determine the apexes of the area of validity as the intersection points between the different straight lines.
- The straight line
- The straight line
- The straight line
Therefore, the apexes of the region of validity are:
Example
Given the set of restrictions:
We look first for the straight lines associated with every restriction and the areas of validity of every inequation (checking it with a point in the inequations). The associatd straight lines are:
Drawing the straight lines and the validity areas we can visualize the validity region.
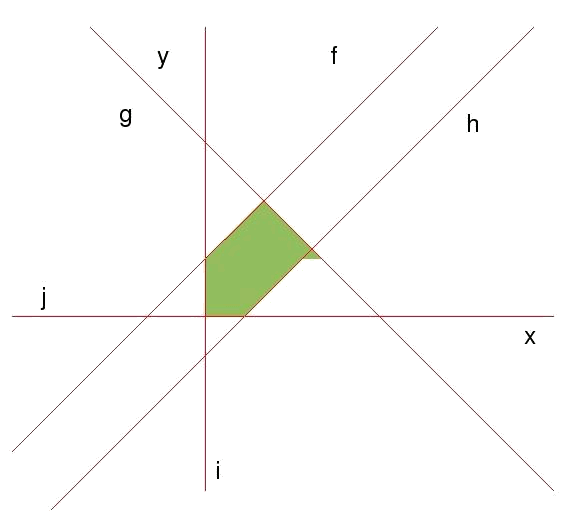
If we cannot do the drawing we have an alternative. Having so many straight lines, normally we will have more intersection points between the straight lines than apexes in the validity area. For this reason, not all the points of intersection between the different straight lines will be apexes of the region of validity. To admit which ones are the apexes of the region of validity the following will be done:
-
All the intersection points are calculated between the different straight lines.
- Those points of intersection where all the restrictions are fulfilled simultaneously will be the apexes of the area of validity (what can allow us to visualize it, if we have not done so before).
Thus, we are going to calculate all the intersection points between the different straight lines.
-
-
-
-
-
-
-
-
-
Determination of the apexes of the area of validity:
We have that nine intersection points between the straight lines. As we have said before, it has to be verified at what points all the inequations are satisfied, and these will be the apexes of the region of validity.
Therefore the apexes of the region of validity are:
To sum up, if we have several inequations simultaneously, each one will determine a semiplane where it is satisfied. The intersection of these semiplanes (common region to all of them) will be called the feasible region, which is the region where all the inequations are satisfied simultaneously. This area can be bounded or not.
We determine the apexes of the area of validity, determining the points of intersection of the straight lines two by two. If we have two straight lines:
The intersection point will be
The solution to this equation is:
And the functions
Where the intersection point is between both straight lines:
In this way we calculate the apexes of the region of validity or feasible region.
