Linear inequations of two variables

Let's begin with a few particular cases:

We have to transport $5$ office chairs (that weigh $10$ kg each one) and three tables (weighing $20$ kg each). We have a truck that can transport $1000$ kg. Obviously, since it is satisfied that the total weight of chairs plus the weight of the tables ( $5 \cdot 10 kg + 3 \cdot 20 kg = 110 kg$ ) is lower than the weight that the truck can transport, it will be possible to do it all in one trip. It is possible to express this mathematically, affirming that the following inequality is satisfied:

$5 \cdot 10 kg + 3 \cdot 20 kg < 1000 kg$

Now we have to transport twenty $10$ kg chairs and $40$ tables of $20$ kg each. This time we have to see if it is satisfied that the total weight of tables plus chairs is lower than or equal to the weight that the truck can transport

$20 \cdot 10 kg + 40 \cdot 20 kg = 1000 kg$

So we will be able to transport everything in just one trip.

Then if we have an indeterminate number $x$ of $10$ kg chairs and a number of tables which is also indeterminate $y$ , we will know that the weight limit that the truck can take in only one trip is:

$x \cdot 10 kg + y \cdot 20 kg ⩽ 1000 kg$

This last expression is what is known as a linear inequation ( $⩽$ ) of two variables ( $x$ and $y$ ). Linear means that the inequation depends only on a linear combination of $x$ and $y$ (no higher power of the variables appears). It is read: the weight of the chairs ( $x \cdot 10$ kg) plus the weight of the tables ( $y \cdot 20$ kg) is equal to or lower than the weight that the truck can transport ( $1000$ kg).

It is interesting to determine what set of points $(x, y)$ satisfy the inequation. To know this, it is possible to draw the inequation in the plane XY. It is necessary to isolate $y$ in the inequation:

$y ⩽ - \frac{10 kg}{20 kg} \cdot x + \frac{1000 kg}{20 kg}$

Taking strictly the equality sign ( $=$ ) we have the equation of a straight line of slope $- \frac{10 kg}{20 kg} = - 0.5$ and ordinate at the origin (that is to say, the point where it crosses the axis $y$ ) $\frac{1000 kg}{20 kg} = 50$ .

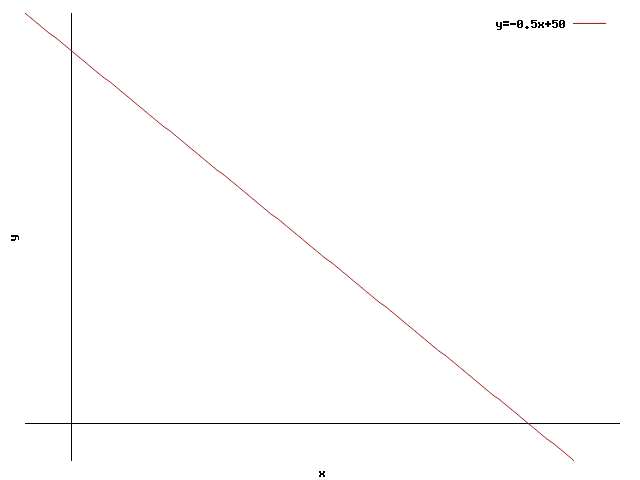
imagen

This straight line separates the points where the inequation is satisfied (the validity regionity) from the points where it is not satisfied. To recognise which side each one is we have to try some point in the inequation to see if it is satisfied or not. For example, it is possible to try with the point $(x = 0, y = 55)$ . The inequation at this point is:

$0 \cdot 10 kg + 55 \cdot 20 kg ⪇ 1000 kg$

In this point the inequation is not satisfied (the right side adds up to $1100$ kg). Therefore the points over the straight line do not satisfy the inequation, while those that are below (or on the straight line) do satisfy it.

imagen

Other examples:

Example

The fishing restrictions imposed by the CEE force a certain company to catch a maximum of $3.000$ tons of hake and angler fish.

First the variables have to be identified. We will call $x$ the hake quantity caught (in tons), and $y$ the angler fish quantity caught (also in tons). So this restriction will be given by the inequation:

$x + y ⩽ 3000$

The straight line associated with this inequation is: $y = - x + 3000$

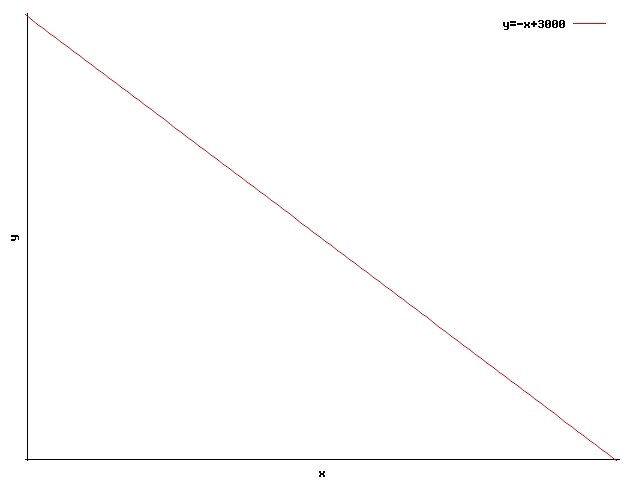
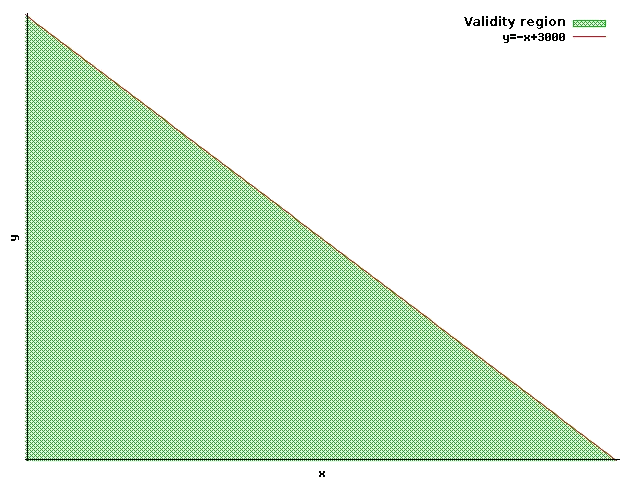
imagen

To know which halves of the plane is the validity region, we have to try a point. Once we have done the test with the point $(x = 0, y = 0)$ :

$0 + 0 ⩽ 3000$

the inequation is satisfied in $(0, 0)$ , therefore the validity region is the one that is below the straight line:

imagen

Example

In a trendy pants factory, there have zippers and holes all along the material, it is controled that every pair of pants has at least three holes.

Like before, first the variables of the problem to be identified. In this case these will be the number of zippers $x$ and the number of holes $y$ . In this case, the restriction will be:

$y ⩾ 3$

We see in this inequation two characteristics distinct from those of the inequations seen before. The first thing that we see is that in the restriction there only appears one of the variables , and the second thing is that this time we have a sign of greater than or equal to ( $⩾$ ), instead of the symbol of smaller than or equal to ( $⩽$ ) even though this inequation has the same properties as the ones that we have already seen. It is possible to see that the straight line associated with this inequation is a constant: $y = 3$

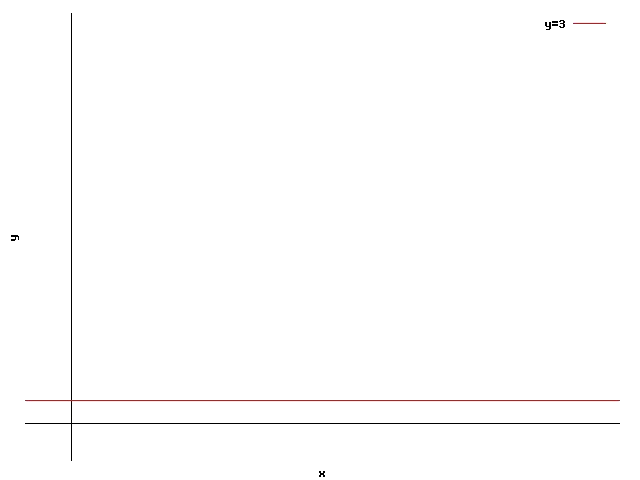
imagen

To know which of the two is the validity region, we try the inequation with the point $(x = 0, y = 0)$ : $0 ⪈ 3$

In $(0, 0)$ the inequation is not satisfied, therefore the validity region is the top semiplane.

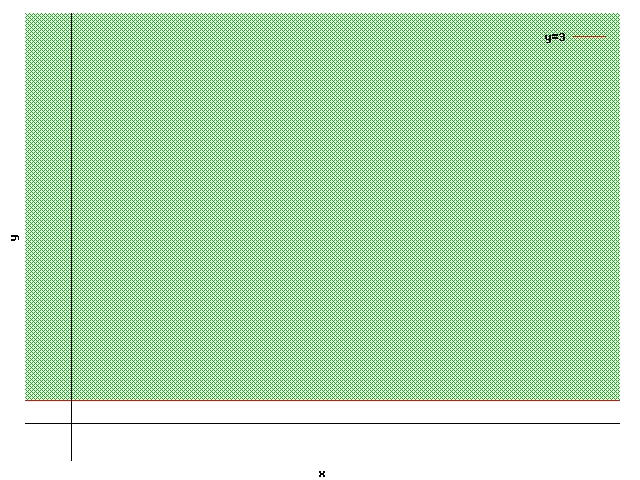
imagen

This was obvious from only seeing the inequation: $y ⩾ 3$ .

Example

A distributor can distribute as many parcels as he can, as long as they do not exceed $200$ km per day.

Again first we identify the variables. We will call $x$ the number of kilometers that he does, and $y$ to the number of parcels that he distributes. In this case the restriction will be the following inequation:

$x ⩽ 200$

In this case it also only depends on one of the variables. We cannot isolate $y$ , because there is no $y$ , but we already know that this restriction will be represented by a vertical straight line (parallel to the axis $y$ ) that separates the values of $x$ higher and smaller than $200$ , and we will take the area of $x$ smaller than or equal to $200$ :

imagen

Example

A pastry cook has $150$ kg of flour to bake two types of cakes P and Q. To make a dozen cakes of type P he needs $3$ kg of flour and to make a dozen of type Q $6$ kg of flour.

The variables are identified first. In this case they will be the number of cakes of the type P ( $x$ ) and the number of cakes of the type Q ( $y$ ). To make a cake of the type P the ingredients that are needed are $\frac{3}{12} kg = \frac{1}{4} kg$ of flour ( $3$ kg that are needed to make $12$ cakes, divided by these $12$ cakes). To make one cake of the type Q the ingredients needed are $\frac{6}{12} kg = \frac{1}{2} kg$ of flour. Thus, the restriction will be that the flour that is used cannot exceed the $150$ kg that the pastry cook has:

$\frac{1}{4} \cdot x + \frac{1}{2} \cdot y ⩽ 150$

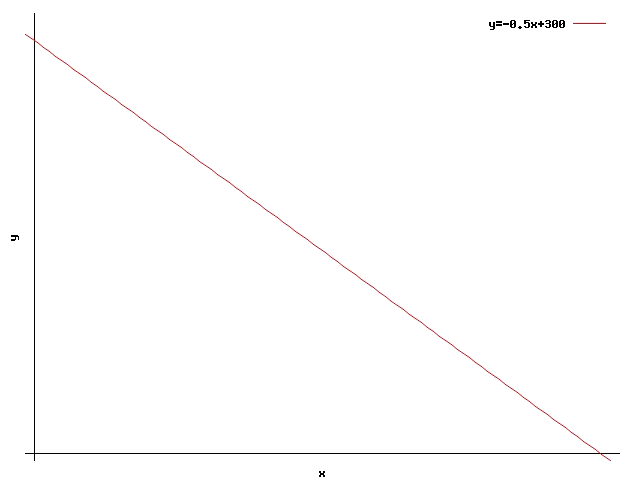
The straight line associated with this inequation is: $y = - \frac{1}{2} \cdot x + 300$

imagen

Now we check if the point $(x = 0, y = 0)$ satisfies the inequation or not, to find out which of two semiplanes is the validity region:

$\frac{1}{4} \cdot 0 + \frac{1}{2} \cdot 0 ⩽ 150$

The inequation is satisfied at point $(0, 0)$ , therefore the validity region is the one that is below the straight line:

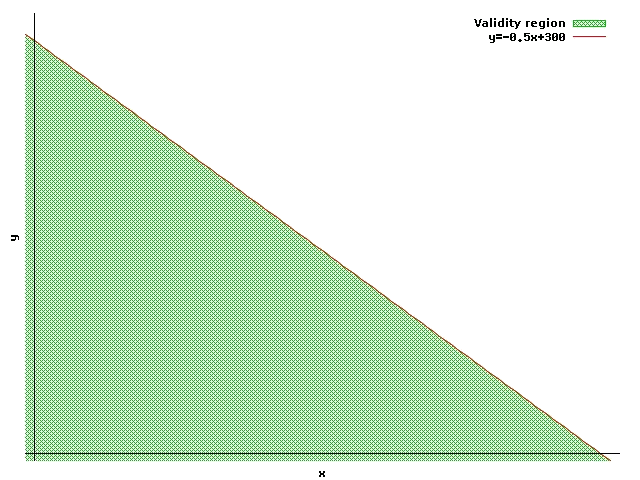
imagen

In short:

When we have a restriction, we will be able to write it as an inequation. First, the variables have to be identified and the inequation has to be written: $a \cdot x + b \cdot y ⩽ c$

The associated straight line will be: $y = - \frac{a}{b} \cdot x + \frac{c}{b}$

(Except in the case where $b = 0$ . In this case the variable Y does not appear in the inequation and the associated straight line is parallel to the axis $y$ , separating the values of $x$ between those that satisfy the inequation and those that do not).

Finally we would have to look at which of the semiplanes in which the straight line separates the plane is the area where the inequation is satisfied (validity region). The easiest way to do this is to see if point $(x = 0, y = 0)$ satisfies the inequation or not. If $(0, 0)$ satisfies the inequation, the area to which it belongs is the validity region. Otherwise, the other area will be the validity region.