Asymptotes of a function

We define an asymptote as a straight line that can be horizontal, vertical or obliquous that goes closer and closer to a curve which is the graphic of a given function.

These asymptotes usually appear if there are points where the function is not defined.

Let's see an example, since it will make it easier to understand.

Example

Let's take the function $f (x) = \frac{1}{x}$ . It is clear that when $x = 0$ the function is not defined. It is exactly here where the asymptote appears. Let's see the graphic representation of this function:

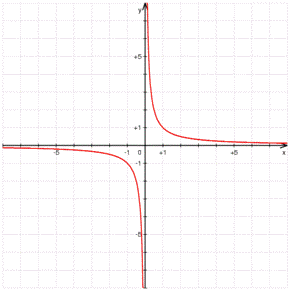
imagen

When we go closer and closer to $x = 0$ from the right we can observe that the function tends to infinity, increasingly approaching the straight line $x = 0$ . The same happens on the other side, but going to minus infinity when approaching the line $x = 0$ . We say that the line $x = 0$ is an asymptote.

Let's see a more exact definition of asymptote of a function $f (x)$ :

Vertical Asymptote

We will say that the straight line $x = a$ (where $a$ is a number) is a vertical asymptote if there exist some of these two limits:

$lim_{x \to a^{-}} f (x) = \pm \infty$
$lim_{x \to a^{+}} f (x) = \pm \infty$

Example

The function $f (x) = \frac{1}{1 + x}$ has a vertical asymptote in $x = - 1$ , since the limit $lim_{x \to - 1^{+}} f (x) = \pm \infty$ exists and therefore the asymptote also does.

imagen

Horizontal Asymptote

If the following limit exists:

$lim_{x \to \pm \infty} f (x) = a$

where $a$ is a finite value, then we will say that the line $y = a$ is an horizontal asymptote.

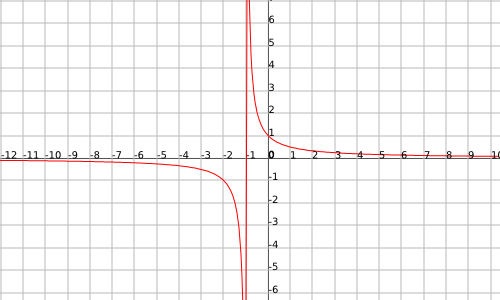
Example

The function $f (x) = e^{x}$ has an horizontal asymptote in $y = 0$ since:

$lim_{x \to - \infty} e^{x} = 0$

Obliquous Asymptote

If the following limits exist and are finite:

$lim_{x \to \infty} \frac{f (x)}{x} = m$
$lim_{x \to \infty} (f (x) - m x) = b$

Then we will say that an obliquous asymptote exists and the line of the asymptote is given by the equation $y = m x + b$ .

The obliquous asymptotes only exist in rational functions (division of polynomials) where the polynomial of the nominator has a greater degree than the denominator.

Example

The function $f (x) = \frac{x^{2} + 1}{x}$ has an obliquous asymptote since the following limits exist:

$m = lim_{x \to \infty} \frac{f (x)}{x} = lim_{x \to \infty} \frac{x^{2} + 1}{x^{2}} = 1$

$b = lim_{x \to \infty} (f (x) - m x) = lim_{x \to \infty} (\frac{x^{2} + 1}{x} - \frac{x^{2}}{x}) = lim_{x \to \infty} (\frac{1}{x}) = 0$

so the line $y = x$ is the obliquous asymptote.

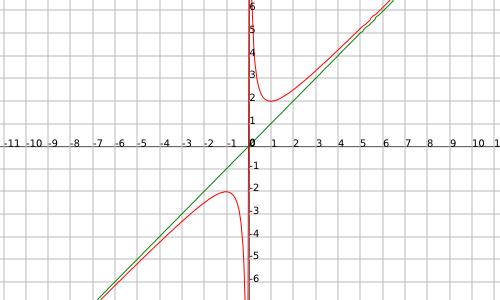
(we observe the obliquous asymptote in green, the straight line being $y = x$ ).