Asímptotes d'una funció

Definim una asímptota com una línia recta que pot ser horitzontal, vertical o obliqua a la qual s'aproxima una corba com a gràfica d'una determinada funció.

Aquestes asímptotes solen aparèixer al haver-hi punts on la funció no estigui definida.

Vegem-ho en un exemple, ja que serà més fàcil d'entendre.

Exemple

Prenguem la funció $f (x) = \frac{1}{x}$ . És clar que quan $x = 0$ tenim un problema de definició. Justament, és aquí on apareix la asímptota. Vegem la representació gràfica d'aquesta funció:

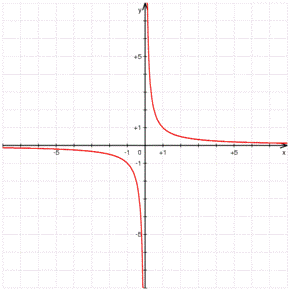
imagen

Podem observar que quan la funció s'aproxima a $x = 0$ per la dreta tendeix a infinit acostant-se cada vegada més a la recta $x = 0$ i per l'esquerra tendeix a menys infinit acostant-se cada vegada més a la mateixa recta $x = 0$ . Llavors diem que $x = 0$ és una asímptota.

Vegem doncs una definició més exacta d'asímptota d'una funció $f (x)$ :

Asímptota vertical

Direm que la recta $x = a$ (on $a$ és una constant) és una asímptota vertical si es compleix alguna d'aquestes dues condicions:

$lim_{x \to a^{-}} f (x) = \pm \infty$
$lim_{x \to a^{+}} f (x) = \pm \infty$

Exemple

La funció $f (x) = \frac{1}{1 + x}$ té una asímptota vertical en $x = - 1$ , ja que el límit $lim_{x \to - 1^{+}} f (x) = \pm \infty$ .

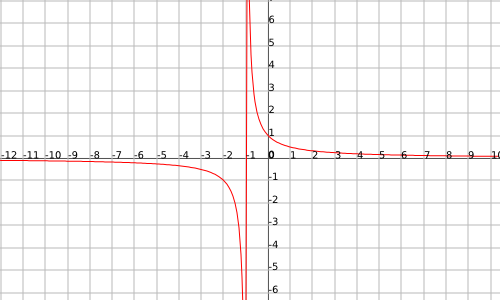
imagen

Asímptota horitzontal

Si existeix el límit:

$lim_{x \to \pm \infty} f (x) = a$

on $a$ és un valor finit, aleshores direm que la recta $y = a$ és una asímptota horitzontal.

Exemple

La funció $f (x) = e^{x}$ té una asímptota horitzontal en $y = 0$ ja que:

$lim_{x \to - \infty} e^{x} = 0$

Asímptota obliqua

Si existeixen els següents límits i són finits:

$lim_{x \to \infty} \frac{f (x)}{x} = m$
$lim_{x \to \infty} (f (x) - m x) = b$

llavors direm que té una asímptota obliqua i la recta de la asímptota obliqua està donada per l'equació $y = m x + b$ .

Les asímptotes obliqües només existeixen en funcions racionals (divisió de polinomis) on el polinomi dividend és d'un grau superior al del polinomi divisor.

Exemple

La funció $f (x) = \frac{x^{2} + 1}{x}$ té asímptota obliqua ja que els límits següents existeixen:

$m = lim_{x \to \infty} \frac{f (x)}{x} = lim_{x \to \infty} \frac{x^{2} + 1}{x^{2}} = 1$

$b = lim_{x \to \infty} (f (x) - m x) = lim_{x \to \infty} (\frac{x^{2} + 1}{x} - \frac{x^{2}}{x}) = lim_{x \to \infty} (\frac{1}{x}) = 0$

i a més la recta $y = x$ és la asímptota obliqua.

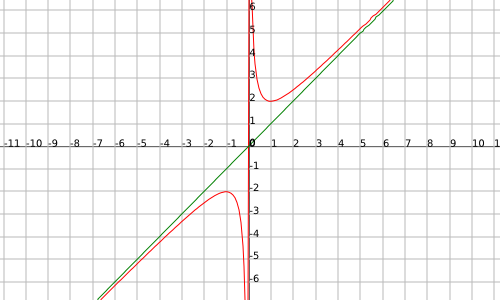
(observem la asímptota obliqua de color verd, la recta $y = x$ ).