Asíntotas de una función

Definimos una asíntota como una línea recta que puede ser horizontal, vertical u oblicua a la que se aproxima una curva como gráfica de una determinada función.

Estas asíntotas suelen aparecer al haber puntos donde la función no esté definida.

Veámoslo en un ejemplo, puesto que resultará de mejor entender:

Ejemplo

Tomemos la función $f (x) = \frac{1}{x}$ . Está claro que cuando $x = 0$ tenemos un problema de definición. Justamente, es aquí donde aparece la asíntota. Veamos la representación gráfica de esta función:

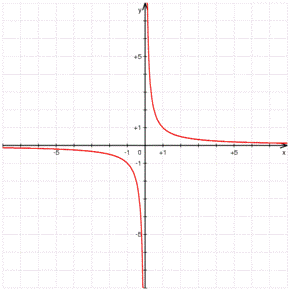
imagen

Podemos observar que cuando la función se aproxima a $x = 0$ por la derecha tiende a infinito acercándose cada vez más a la recta $x = 0$ y por la izquierda tiende a menos infinito acercándose cada vez más a la misma recta $x = 0$ . Entonces decimos que $x = 0$ es una asíntota.

Veamos pues una definición más exacta de asíntota de una función $f (x)$ :

Asíntota vertical

Diremos que la recta $x = a$ (donde $a$ es un número) es una asíntota vertical si existen algunos de estos dos límites:

$lim_{x \to a^{-}} f (x) = \pm \infty$
$lim_{x \to a^{+}} f (x) = \pm \infty$

Ejemplo

La función $f (x) = \frac{1}{1 + x}$ tiene una asíntota vertical en $x = - 1$ , ya que al existir el límite $lim_{x \to - 1^{+}} f (x) = \pm \infty$ existe la asíntota.

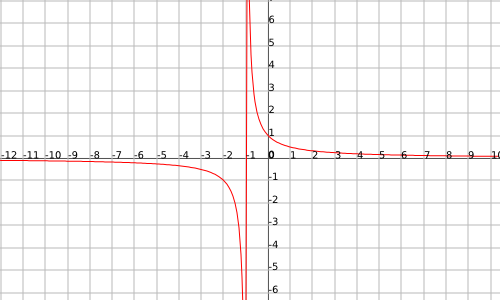
imagen

Asíntota horizontal

Si existe el límite:

$lim_{x \to \pm \infty} f (x) = a$

donde $a$ es un valor finito, entonces diremos que la recta $y = a$ es una asíntota horizontal.

Ejemplo

La función $f (x) = e^{x}$ tiene una asíntota horizontal en $y = 0$ ya que:

$lim_{x \to - \infty} e^{x} = 0$

Asíntota oblicua

Si existen los siguientes límites y son finitos:

$lim_{x \to \infty} \frac{f (x)}{x} = m$
$lim_{x \to \infty} (f (x) - m x) = b$

entonces diremos que exite una asíntota oblicua y la recta de la asíntota oblicua está dada por la ecuación $y = m x + b$ .

Las asíntotas oblicuas sólo existen en funciones racionales (división de polinomios) donde el polinomio dividendo es de un grado superior al del polinomio divisor.

Ejemplo

La función $f (x) = \frac{x^{2} + 1}{x}$ tiene asíntota oblicua ya que los límites siguientes existen:

$m = lim_{x \to \infty} \frac{f (x)}{x} = lim_{x \to \infty} \frac{x^{2} + 1}{x^{2}} = 1$

$b = lim_{x \to \infty} (f (x) - m x) = lim_{x \to \infty} (\frac{x^{2} + 1}{x} - \frac{x^{2}}{x}) = lim_{x \to \infty} (\frac{1}{x}) = 0$

y además la recta $y = x$ es la asíntota oblicua.

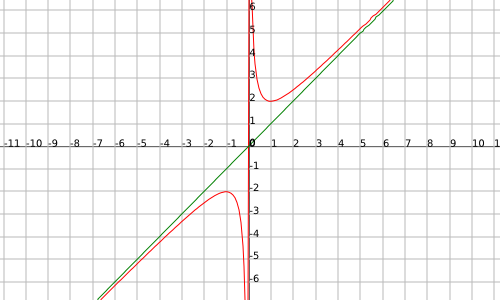
(observamos la asíntota oblicua de color verde, siendo la recta $y = x$ ).