Simetría de una función
Como nos podemos imaginar, las funciones pueden hacer diferentes formas y algunas de ellas son simétricas, otras antisimétricas y otras simplemente tienen formas variadas que no presentan ningún tipo de simetría.
Las simetrías siempre dependen de un eje (el espejo donde haríamos la simetría). Así que una función simétrica debe cumplir la siguiente condición:
Si $$f(x)$$ es función simétrica respecto el eje $$x=x_0$$, entonces se cumple que: $$$ f(x+x_0)=f(-x+x_0)$$$
Particularmente, si tenemos simetría en el eje $$x=0$$, tenemos que $$f(x)=f(-x)$$.
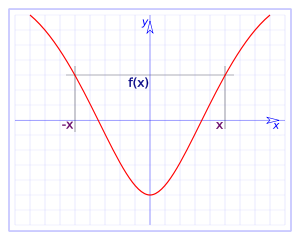
Tradicionalmente y por convenio, se dice que una función par es aquella que cumple $$f(x)=f(-x)$$ (es decir que es simetrica en el eje $$x = 0$$).
Por otra parte, podemos encontrar las funciones antisimétricas, que son funciones que tienen una casi-simetría respecto un eje $$x=x_0$$y que en lugar de ser simétricas, son simétricas pero invertidas, es decir, con valores negativos (multiplicados por $$-1$$).
Estas funciones cumplen pues la condición: $$$f(x+x_0)=-f(-x+x_0)$$$
Particularment, si tenemos antisimetría en el eje $$x = 0$$, tenemos que $$f(x)=-f(-x)$$.
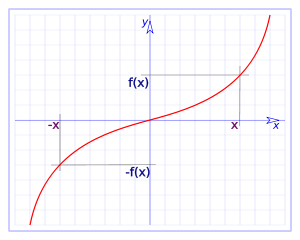
También tradicionalmente y por convenio, se dice que una función impar es aquella que cumple $$f(x)=-f(-x)$$ (antisimetría en eje $$x = 0$$).
Observemos que las funciones antisimétricas cumplen que en el punto del eje de simetría $$x=x_0$$ cumplen que $$f(x_0)=0$$, ya que si $$x=0$$: $$$ f(x+x_0)=-f(-x+x_0) \Rightarrow f(x_0)=-f(x_0) \Rightarrow 2f(x_0)=0 \Rightarrow$$$ $$$\Rightarrow f(x_0)=0$$$
Veamos pues ejemplos de funciones simétricas y antisimétricas:
La función $$f(x)=x^2$$ es un claro ejemplo de función par, ya que $$$ f(-x)=(-x)^2=(-1)^2 x^2=x^2=f(x) $$$
La función $$f(x)=x^3$$ es un ejemplo de función impar, ya que
$$$ f(-x)=(-x)^3=(-1)^3 x^3=-1\cdot x^3=-x^3=-f(x) $$$
La función $$f(x) = 2x-4$$ es una función antisimétrica respecto del eje $$x = 2$$ (ja que $$f(2) = 0$$) y lo podemos comprobar:
$$$ f(-x+2)=2(-x+2)-4=-2x+4-4=-2x-4+4=-2(x+2)+4$$$ $$$=-(2(x+2)-4)=-f(x+2) $$$
La función $$f(x)=(x-1)^2$$ es una función simétrica respecto $$x=1$$:
$$$f(-x+1)=(-x+1-1)^2=(-x)^2=x^2=(x+1-1)^2=f(x+1)$$$
Funciones periódicas
Llamaremos funciones periódicas aquellas que van repitiendo un trozo de función de manera continuada y repetitiva.
Podemos además decir que una función periódica tendrá período $$T$$ ssi cumple que:
$$$f(x+T)=f(x)$$$
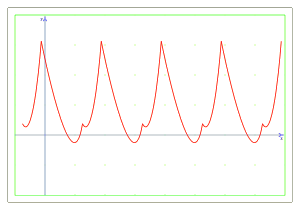
En el dibujo podemos ver claramente un comportamiento periódico de la función.
Veamos unos ejemplos de funciones periódicas:
La función $$f(x)=c$$ donde $$c$$ és una constant es una constante es periódica y de cualquier período ya que es una función constante.
La función $$f(x)=\sin(x)$$ es periódica y su período es $$2\pi$$, ya que: $$$f(x+2\pi)=\sin(x+2\pi)=sin(x)=f(x)$$$
Puntos de corte con los ejes
Cuando tenemos que representar una función, muchas veces resulta muy cómodo saber en que punto exacto corta la función los dos ejes, el de las $$x$$ y el de las $$y$$.
Para saber exactamente en que punto corta, debemos seguir el siguiente procedimiento:
- Corte con el eje $$Y$$: Cuando la función corta el eje $$Y$$ significa que esta en un punto donde $$x=0$$, así que tenemos que buscar el valor de $$f(0)$$ y ese valor será el punto de corte con el eje $$Y$$. Fijémonos en que solo habrá un punto de corte con el eje $$Y$$, ya que si hubiera más de un punto, no sería una función.
Tomemos la función $$f(x)=x^2+x+1+e^x$$. Buscaremos el punto de corte con el eje $$Y$$ valuando la función en el cero: $$$ f(0)=0^2+0+1+e^0=1+1=2$$$
Por consiguiente diremos que la función pasa por el punto $$(0,2)$$ cortando el eje $$Y$$ en el punto $$2$$.
- Corte con el eje $$X$$: cuando la función corte el eje $$X$$ significa que nos encontramos encima de la recta $$y = 0$$, así que debemos imponer la condición $$f(x)=0$$ y solucionar la ecuación aislando la $$x$$. Puede ser que encontremos que hay más de una solución lo que significaría que se corta el eje $$X$$ más de una vez.
Tomemos la función $$f(x)=x^2-1$$. Si queremos encontrar los puntos de corte con el eje $$X$$ debemos imponer que $$f(x)=0$$, por lo tanto: $$$ 0=f(x)=x^2-1 \Rightarrow x^2=1 \Rightarrow x=\pm 1$$$
Resulta que hemos encontrado dos puntos, el $$(1,0)$$ y el $$(-1,0)$$ ssituados encima del eje $$X$$ por donde pasa la función.
