Simetria d'una funció
Com ens podem imaginar, les funcions poden fer diferents formes i algunes d'elles són simètriques, altres antisimètriques i altres simplement tenen formes variades que no presenten cap tipus de simetria.
Les simetries sempre depenen d'un eix (el mirall on faríem la simetria). Així que una funció simètrica ha de complir la següent condició:
Si $$f(x)$$ és funció simètrica respecte l'eix $$x=x_0$$, llavors es compleix que: $$$ f(x+x_0)=f(-x+x_0)$$$
Particularment, si tenim simetria en l'eix 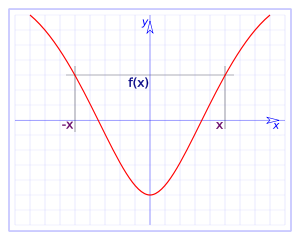$$x=0$$, tenim que $$f(x)=f(-x)$$.
Tradicionalment i per conveni, es diu que una funció parella és aquella que compleix $$f(x)=f(-x)$$ (és a dir que és simètrica a l'eix $$x = 0$$).
D'altra banda, podem trobar les funcions antisimètriques, que són funcions que tenen una quasi-simetria respecte un eix $$x=x_0$$ i que en lloc de ser simètriques, són simètriques però invertides, és a dir, amb valors negatius (multiplicats per $$-1$$).
Aquestes funcions compleixen la condició: $$$f(x+x_0)=-f(-x+x_0)$$$
Particularment, si tenim antisimetria en l'eix $$x = 0$$, tenim que $$f(x)=-f(-x)$$.
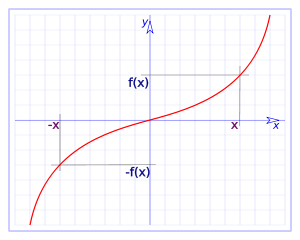
També tradicionalment i per conveni, es diu que una funció senar és aquella que compleix $$f(x)=-f(-x)$$ (antisimetria en l'eix $$x = 0$$).
Observem que les funcions antisimètriques compleixen que en el punt $$x=x_0$$ de l'eix de simetria $$f(x_0)=0$$, ja que si $$x=0$$: $$$ f(x+x_0)=-f(-x+x_0) \Rightarrow f(x_0)=-f(x_0) \Rightarrow 2f(x_0)=0 \Rightarrow$$$ $$$\Rightarrow f(x_0)=0$$$
Vegem exemples de funcions simètriques i antisimètriques.
La funció $$f(x)=x^2$$ és un clar exemple de funció parella, ja que $$$ f(-x)=(-x)^2=(-1)^2 x^2=x^2=f(x) $$$
La funció $$f(x)=x^3$$ és un clar exemple de funció senar, ja que $$$ f(-x)=(-x)^3=(-1)^3 x^3=-1\cdot x^3=-x^3=-f(x) $$$
La funció $$f(x) = 2x-4$$ és una funció antisimètrica respecte de l'eix $$x = 2$$ (ja que $$f(2) = 0$$) i ho podem comprovar:
$$$ f(-x+2)=2(-x+2)-4=-2x+4-4=-2x-4+4=-2(x+2)+4$$$ $$$=-(2(x+2)-4)=-f(x+2) $$$
La funció $$f(x)=(x-1)^2$$ és una funció simètrica respecte $$x=1$$:
$$$f(-x+1)=(-x+1-1)^2=(-x)^2=x^2=(x+1-1)^2=f(x+1)$$$
Funcions periòdiques
Anomenarem funcions periòdiques aquelles que van repetint un tros de funció de manera continuada i repetitiva.
Podem a més dir que una funció periòdica tindrà període $$T$$ si compleix que:
$$$f(x+T)=f(x)$$$
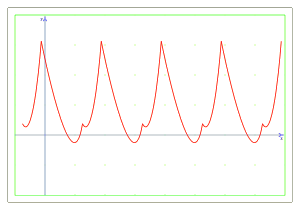
En el dibuix podem veure clarament un comportament periòdic de la funció.
Vegem uns exemples de funcions periòdiques.
La funció $$f(x)=c$$ on $$c$$ és una constant és periòdica i de qualsevol període ja que és una funció constant.
La funció $$f(x)=\sin(x)$$ és periòdica i el seu període és $$2\pi$$, ja que: $$$f(x+2\pi)=\sin(x+2\pi)=sin(x)=f(x)$$$
Punts de tall amb els eixos
Quan hem de representar una funció, moltes vegades resulta molt còmode saber en quin punt exacte talla la funció els dos eixos, el de les $$x$$ i el de les $$y$$.
Per saber exactament en quin punt talla, hem de seguir el següent procediment:
- Tall amb l'eix $$Y$$: Quan la funció talla l'eix $$Y$$ vol dir que està en un punt on $$x=0$$, així que hem de buscar el valor de $$f(0)$$ i aquest valor serà el punt de tall amb l'eix $$Y$$. Fixem-nos que només hi haurà un punt de tall amb l'eix $$Y$$, ja que si n'hi hagués més d'un, no seria una funció.
Vegem un exemple:
Prenguem la funció $$f(x)=x^2+x+1+e^x$$. Buscarem el punt de tall amb l'eix $$Y$$ avaluant la funció en el zero: $$$ f(0)=0^2+0+1+e^0=1+1=2$$$
Per tant direm que la funció passa pel punt $$(0,2)$$ tallant l'eix $$Y$$ en el punt $$2$$.
- Tall amb l'eix $$X$$: quan la funció talla l'eix $$X$$ vol dir que ens trobem sobre de la recta $$y = 0$$, així que hem de imposar la condició $$f(x)=0$$ i solucionar l'equació aïllant la $$x$$. Pot ser que trobem que hi ha més d'una solució, el que significaria que es talla l'eix $$X$$ més d'una vegada.
Vegem un exemple:
Prenguem la funció $$f(x)=x^2-1$$. Si volem trobar els punts de tall amb l'eix $$X$$ hem d'imposar que $$f(x)=0$$, per tant: $$$ 0=f(x)=x^2-1 \Rightarrow x^2=1 \Rightarrow x=\pm 1$$$
Resulta que hem trobat dos punts, el $$(1,0)$$ i el $$(-1,0)$$ situats sobre l'eix $$X$$ per on passa la funció.