Creixement i decreixement
Les funcions poden ser creixents o decreixents al llarg del seu domini o en un cert interval.
Diem que una funció
Diem que una funció
Les funcions que mai decreixen, sempre augmenten el seu valor o es mantenen (les funcions creixents).
Anàlogament, les funcions decreixents mai creixen, sempre disminueixen el seu valor o es mantenen quan
D'altra banda, podem definir funcions estrictament creixents o decreixents: aquestes mai es mantindran en un mateix valor: o augmenten o disminueixen.
Diem que una funció
A continuació podem veure uns exemples:
Exemple
Totes les funcions del tipus
Exemple
La funció
Exemple
Les funcions constants són funcions que alhora són creixents i decreixents (es mantenen constants).
Màxims i mínims
Quan representem una funció podem veure que de vegades apareixen punts que són màxims o mínims relatius o globals.
Com podem veure en el següent exemple, podem observar que en 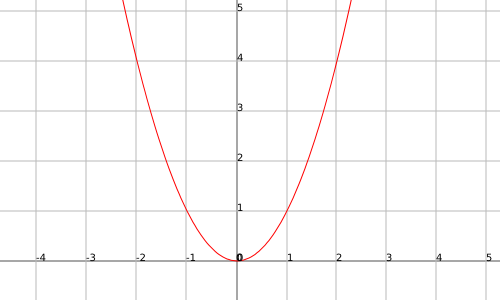
Definim doncs correctament el concepte de mínim i màxim relatiu i global:
- Un punt
- Un punt
- Un punt
- Un punt
Per entendre millor cada concepte vegem un exemple de cada:
Exemple
La funció
Exemple
La funció 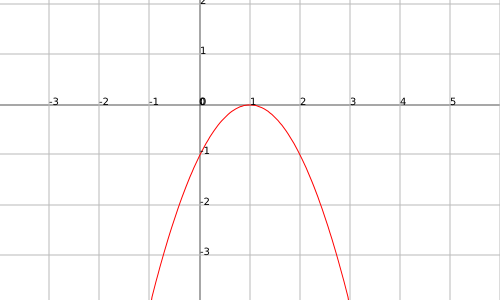
Exemple
La funció 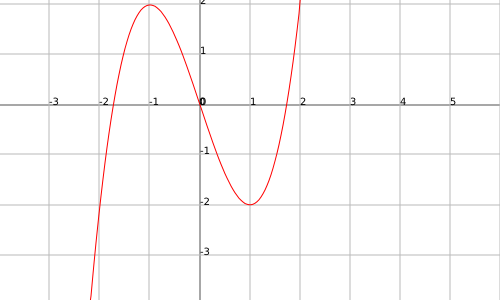
Exemple
La funció 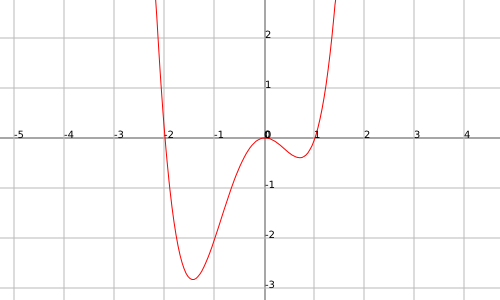
Localització de màxims i mínims
Anem a veure com trobar màxims i mínims relatius.
Per això considerem una funció
Si ens fixem en les gràfiques anteriors, els punts màxims i mínims relatius tenen com a recta tangent una recta de pendent zero. Aquesta serà la clau per trobar màxims i mínims.
El procediment serà derivar la funció
El següent pas serà saber si són màxims o mínims. Això es pot deduir del valor que prengui la segona derivada de la funció en el punt en qüestió: si és positiu, serà mínim, i si és negatiu, serà màxim.
Per entendre bé el procés, vegem un exemple.
Exemple
Prenguem la funció
Començarem derivant la funció i igualant a zero. Resoldrem l'equació i ens quedarem amb els punts solució.
Ara sabem que en els punts
i per tant en
Vegem la gràfica per veure clarament l'exemple:

