Crecimiento y decrecimiento
Las funciones pueden ser crecientes o decrecientes a lo largo de su dominio o en un cierto intervalo.
Decimos que una función $$f(x)$$ es creciente en el intervalo $$[a,b]$$ si dados dos puntos de $$[a,b]$$, $$x_1$$ y $$x_2$$ tal que $$x_1 < x_2$$ entonces $$f(x_1) \leqslant f(x_2)$$.
Decimos que una función $$f(x)$$ es decreciente en intervalo $$[a,b]$$ ssi dados dos puntos de $$[a,b]$$, $$x_1$$ y $$x_2$$ tal que $$x_1 < x_2$$ entonces $$f(x_1) \geqslant f(x_2)$$.
Las funciones que nunca decrecen, siempre aumentan su valor o se mantienen (las funciones crecientes).
Análogamente, las funciones decrecientes nunca crecen, siempre disminuyen su valor o se mantienen cuando $$x$$ se hace grande.
Por otra parte, podemos definir funciones estrictamente crecientes o decrecientes: éstas nunca se mantendrán en un mismo valor: o aumentan o disminuyen.
Decimos que una función $$f(x)$$ es estrictamente creciente en el intervalo $$[a,b]$$ si dados dos puntos de $$[a,b]$$, $$x_1$$ y $$x_2$$ tal que $$x_1 < x_2$$ entonces $$f(x_1) < f(x_2)$$.
Decimos que una función $$f(x)$$ es estrictamente decreciente en el intervalo $$[a,b]$$ si dados dos puntos de $$[a,b]$$, $$x_1$$ y $$x_2$$ tal que $$x_1 < x_2$$ entonces $$f(x_1) > f(x_2)$$.
A continuación podemos ver unos ejemplos:
Todas las funciones del tipo $$f(x)=ax+b$$ cuando $$a>0$$ son funciones crecientes, y en particular, son funciones estrictamente crecientes. No obstante, cuando tomemos $$a < 0$$ obtendremos funciones estrictamente decrecientes (y por consiguiente decrecientes).
La función $$f(x)=x^2$$ es una función decreciente en el intervalo $$(-\infty,0]$$ y creciente en $$[0,+\infty)$$.
Las funciones constantes son funciones que a la vez son crecientes y decrecientes (se mantienen constantes).
Máximos y mínimos
Cuando representamos una función podemos ver que a veces aparecen puntos que son máximos o mínimos relativos o globales.
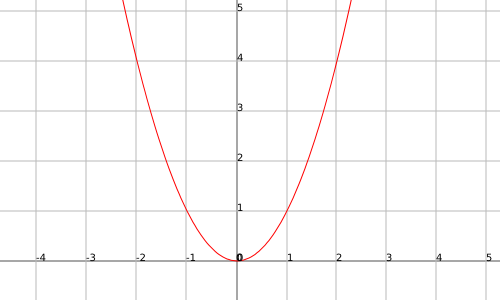
Como podemos ver en el siguiente ejemplo, podemos observar que en $$x=0$$ la función $$f(x)=x^2$$ tiene un mínimo:
Definamos pues correctamente el concepto de mínimo y máximo relativo y global:
- Un punto $$x_0$$ se denomina máximo global si para todo punto $$x$$ del dominio, la función comple $$f(x)\leqslant f(x_0)$$.
- Un punto $$x_0$$ se denomina mínimo global si para todo punto $$x$$ del dominio, la función comple $$f(x)\geqslant f(x_0)$$.
- Un punto $$x_0$$ se denomina máximo relativo si para todo punto $$x$$ de un entorno de $$x_0$$ $$\ [x_0-\varepsilon,x_0+\varepsilon]$$ (donde $$\varepsilon$$ es un valor pequeño), la función comple $$f(x)\leqslant f(x_0)$$.
- Un punto $$x_0$$ se denomina mínimo relativo si para todo punto $$x$$ de un entorno de $$x_0$$ $$\ [x_0-\varepsilon,x_0+\varepsilon]$$ (donde $$\varepsilon$$ es un valor pequeño), la función comple $$f(x)\geqslant f(x_0)$$.
Para entender mejor cada concepto veamos un ejemplo de cada:
La función $$f(x)=x^2$$ presenta un mínimo global en el punto $$x=0$$ (ver ejemplo previo a las definiciones).
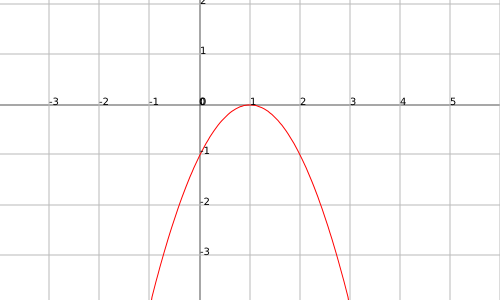
La función $$f(x)=-(x-1)^2$$ presenta un màximo global en el punto $$x=1$$:
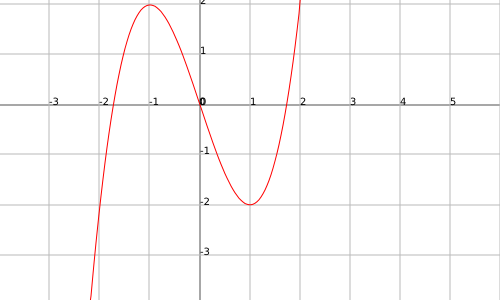
La función $$f(x)=x^3-3x$$ presenta un màximo relativo en $$x=-1$$ y un mínimo relativo en $$x=1$$:
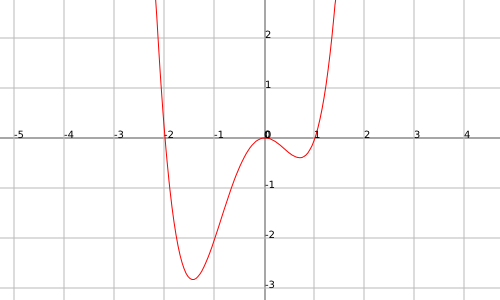
La función $$f(x)=x^4-x^3-2x^2$$ presenta un mínimo global en el intervalo $$[-2, -1]$$, tiene un máximo relativo en $$x=0$$ y un mínimo relativo en el intervalo $$(0,1)$$:
Localización de màximos y mínimos
Vamos a ver cómo encontrar máximos y minimos relativos.
Para ello consideramos una función $$f(x)$$ c contínua en un dominio abierto y derivable en éste.
Si nos fijamos en las gráficas anteriores, los puntos máximos y mínimos relativos tienen como recta tangente una recta de pendiente cero. Esta será la clave para encontrar máximos y mínimos.
El procedimiento será derivar la función $$f(x)$$ y igualarla a cero. Resolviendo la ecuación que aparece encontraremos los puntos $$x$$ que serán máximos o mínimos en nuestra función.
El siguiente paso será saber si son máximos o mínimos. Esto se puede deducir del valor que alcance la segunda derivada de la función en el punto en cuestión: si es positivo, será mínimo, y si es negativo, será máximo.
Para entender bien el proceso, veamos un ejemplo.
Tomemos la función $$f(x)=x^3-3x$$.
Empezaremos derivando la función y igualandola a cero. Resolveremos la ecuación y nos quedaremos con los puntos solución. $$$f'(x)=3x^2-3 \Rightarrow 3x^2-3=0 \Rightarrow x^2=1 \Rightarrow x=\pm1$$$
Ahora sabemos que en los puntos $$1$$ y $$-1$$ tenemos máximos o mínimos. Vamos a ver qué son usando la segunda derivada: $$f''(x)=6x$$:
$$f''(1)=6 > 0$$
$$f''(-1)=-6 < 0$$
y por lo tanto, en $$x =- 1$$ tenemos máximo y en $$x = 1$$ tenemos un mínimo.
Veamos el gráfico para ver claramente el ejemplo:

