Representación gráfica de una función

Dada una función $f (x)$ definida $\begin{array}{rcl} f : X & ⟶ & Y \\ x & ⟼ & f (x) = y \end{array}$

definimos la gráfica de esta función como el conjunto de puntos: ${(x, y) \in X \times Y | y = f (x)}$ o también los pares de puntos $(x, f (x))$ . Estos puntos se pueden representar con coordenadas cartesianas en el plano $X Y$ formándose así el dibujo de la gráfica de la función $f (x)$ .

Ejemplo

Tomemos la función $f (x) = x^{3}$ . Su gráfica vendrá dada por el conjunto de puntos ${(x, f (x))} = {(x, x^{3})}$ variando el valor de $x$ .

Si lo representamos obtenemos el dibujo: imagen

Pero, ¿Cómo se representa una gráfica? Para poder explicarlo debemos introducir antes el concepto de dominio e imagen de una función.

En una función $f (x)$ distinguimos dos conjuntos: uno es el conjunto de donde tomamos valores para evaluar la función (los posibles valores de $x$ ) y el otro es el conjunto formado por los diferentes valores que alcanza la función $f (x)$ .

Entonces, definimos:

Dominio de una función como el conjunto de valores donde evaluaremos la función. Se denota como: $Dom (f)$ .
Imagen de una función como el conjunto de valores obtenidos por la función. Se denota como: $Im (f)$ .

Fijémonos que cuando notamos una función como: $\begin{array}{rcl} f : X & ⟶ & Y \\ x & ⟼ & f (x) = y \end{array}$

el conjunto $X$ es el dominio, puesto que tomaremos los valores de $x$ de dentro de éste y la imagen estaría dentro del conjunto $Y$ .

Veámoslo mejor con algunos ejemplos:

Ejemplo

La función $f (x) = x$ tiene como dominio toda la recta real, puesto que podemos evaluarla en cualquier punto, y tiene como imagen la misma recta, ya que la función es la identidad.

Por lo tanto escribiremos:

$Dom (f) = R = (- \infty, \infty)$

$Im (f) = R = (- \infty, \infty)$

Ejemplo

La función té $f (x) = x^{2}$ tiene como dominio también toda la recta real (podemos evaluarla en cualquier punto) y no obstante, al ser la función "elevar al cuadrado", sólo obtenemos valores positivos. Por consiguiente su imagen será la semirecta real positiva incluyendo el cero.

Por lo tanto escribiremos:

$Dom (f) = R = (- \infty, \infty)$

$Im (f) = [0, \infty)$

Podemos observar que el dominio puede ser un conjunto a elección nuestra (ya que podemos escogerlo más pequeño o más grande) mientras que la imagen vendrá dada por el dominio escogido.

A veces, pero, nos encontramos que nuestra función por ciertos motivos no puede ser evaluada en ciertos puntos ya que no está definida, así que tendremos que excluir ciertos puntos o intervalos del dominio.

Ejemplo

Si tomamos la función $f (x) = \frac{x + 1}{x} + 1$ podemos ver que cuando $x = 0$ tenemos la expresión $\frac{1}{0}$ y esta división no puede realizarse.

Por consiguiente, el dominio de esta función será todos los reales exceptuando el cero:

$Dom (f) = R ∖ {0} = (- \infty, 0) \cup (0, \infty)$

Y la imagen será

$Im (f) = R ∖ {1} = (- \infty, 1) \cup (1, \infty)$

Cálculo de dominios:

Para calcular el dominio de una función tenemos que partir de que puede ser cualquier número de la recta real ( $R$ ) e ir restringiendo el conjunto dependiendo de la función. Para hacer estas restricciones debemos localizar los puntos "débiles" de nuestras funciones o mejor dicho, los puntos de no definición. A continuación listamos los conjuntos de no definición de las principales funciones:

Función	Conjunto de no definición
$f (x) = \log (g (x))$	${x \| g (x) ⩽ 0} =$ los valores de $x$ tal que $g (x)$ se hace negativa o cero
$f (x) = \sqrt{g (x)}$	${x \| g (x) < 0} =$ los valores de $x$ tal que $g (x)$ se hace negativa
$f (x) = \frac{g (x)}{h (x)}$	${x \| h (x) = 0} =$ los valores de $x$ tal que $h (x)$ vale cero
$f (x) = \sqrt[2 n]{g (x)}$	${x \| g (x) < 0} =$ los valores de $x$ tal que $g (x)$ se hace negativa

Ejemplo

Si tomamos la función $f (x) = (\frac{2 x + 1}{x - 4} - \ln (x + 8)) \cdot \sqrt{x^{2} + 1}$ y queremos encontrar su dominio debemos considerar que es toda la recta real y irla restringiendo según encontremos puntos o intervalos de no definición.

En este caso, observamos que tenemos 3 posibles intervalos de no definición:

cuando $x - 4$ sea cero $\Rightarrow x - 4 = 0 \Rightarrow x = 4$ la función no estará definida.
cuando $x + 8$ sea negativo o cero $\Rightarrow x + 4 ⩽ 0 \Rightarrow x ⩽ - 8$ la función no estará definida.
cuando $x^{+} 1$ sea negatvo $\Rightarrow x^{2} + 1 < 0 \Rightarrow x^{2} < - 1$ , cosa que no puede pasar ya que $x^{2}$ siempre es positivo, por lo tanto la función no tiene intervalos de no definición.

Entonces, podemos concluir que el dominio de nuestra función será: $Dom (f) = (- 8, 4) \cup (4, \infty)$

Representación gráfica

Supongamos que tenemos una función $f (x)$ . Para representarla gráficamente debemos primero encontrar su dominio para saber en que puntos debemos evaluarla.

UUna vez encontrado el dominio procederemos a hacer la representación. ¿Cómo lo haremos? Bien, la manera más simple y sencilla es mediante una tabla de valores, es decir, daremos valores a la variable $x$ y encontraremos el valor de $f (x)$ y dibujaremos el punto encontrado, $(x, f (x))$ en el plano usando las coordenadas cartesianas.

Ejemplo

Tomemos la función $f (x) = 2 x + 1$ y vamos a hacer la tabla de valores:

$x$	$f (x)$
$- 2$	$f (2) = 2 \cdot (- 2) + 1 = - 3$
$- 1$	$f (2) = 2 \cdot (- 1) + 1 = - 1$
$0$	$f (2) = 2 \cdot (0) + 1 = 1$
$1$	$f (2) = 2 \cdot (1) + 1 = 3$
$2$	$f (2) = 2 \cdot (2) + 1 = 5$

y por lo tanto encontramos los pares de puntos:

$x$	$f (x)$
$- 2$	$- 3$
$- 1$	$- 1$
$0$	$1$
$1$	$3$
$2$	$5$

los que dibujaremos en el plano $X Y$ y eos uniremos con una línea. Al final obtenemos:

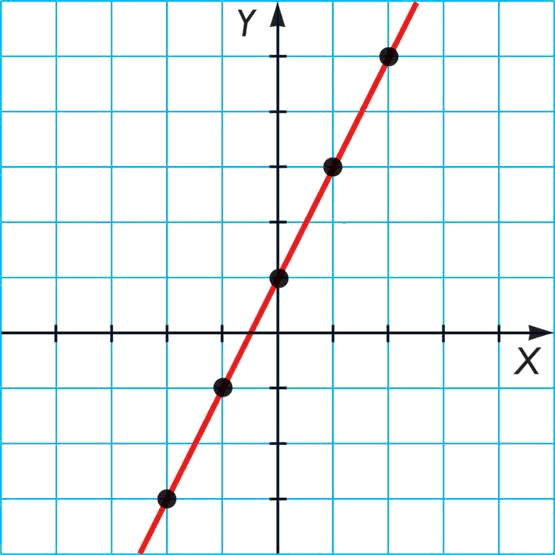
imagen

donde hemos marcado con puntos las coordenadas encontradas en la tabla de valores.

Este procedimiento (hacer la tabla de valores) puede sernos muy útil cuando debemos dibujar una función, pero a veces nos puede desconcertar, ya que existen funciones muy diversas y a veces sólo encontrando unos cuantos puntos en la tabla de valores no basta para poder dibujar la función.