Donada una funció $$f(x)$$ definida $$$ \begin{array}{rcl} f: X & \longrightarrow &Y \\ x &\longmapsto & f(x)=y \end{array} $$$
definim la gràfica d'aquesta funció com el conjunt de punts: $$$ \{ (x,y)\in X\times Y \ | \ y=f(x) \} $$$ o també els parells de punts $$(x,f(x))$$. Aquests punts es poden representar amb coordenades cartesianes en el pla $$XY$$ formant-se així el dibuix de la gràfica de la funció $$f(x)$$.
Prenguem la funció $$f(x)=x^3$$. La seva gràfica vindrà donada pel conjunt de punts $$ \{ (x,f(x))\}=\{(x,x^3)\} $$ variant el valor de $$x$$.
Si ho representem obtenim el dibuix:
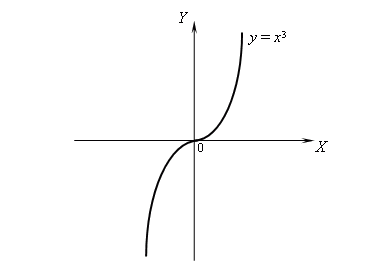
Però, com es representa una gràfica? Per poder explicar-ho hem d'introduir abans el concepte de domini i imatge d'una funció.
En una funció $$f(x)$$ distingim dos conjunts: un és el conjunt d'on prenem valors per avaluar la funció (els possibles valors de $$x$$) i l'altre és el conjunt format pels diferents valors que assoleix la funció $$f(x)$$.
Definim:
- Domini d'una funció com el conjunt de valors on avaluarem la funció. Es denota com: $$\text{Dom}(f)$$.
- Imatge d'una funció com el conjunt de valors obtinguts per la funció. Es denota com: $$\text{Im}(f)$$.
Fixem-nos que quan notem una funció com: $$$ \begin{array}{rcl} f: X & \longrightarrow &Y \\ x &\longmapsto & f(x)=y \end{array} $$$
el conjunt $$X$$ és el domini, ja que prendrem els valors de $$x$$ de dins d'aquest i la imatge estaria dins el conjunt $$Y$$.
Vegem-ho millor amb alguns exemples:
La funció $$f(x)=x$$ té com a domini tota la recta real, ja que podem avaluar en qualsevol punt, i té com a imatge la mateixa recta, ja que la funció és la identitat.
Per tant escriurem:
$$\text{Dom}(f)=\mathbb{R}=(-\infty,\infty)$$
$$\text{Im}(f)=\mathbb{R}=(-\infty,\infty)$$
La funció té $$f(x)=x^2$$ té com a domini també tota la recta real (podem avaluar en qualsevol punt) i no obstant això, en ser la funció "elevar al quadrat", només obtenim valors positius. Per tant la seva imatge serà la semirecta real positiva incloent el zero.
Per tant escriurem:
$$\text{Dom}(f)=\mathbb{R}=(-\infty,\infty)$$
$$\text{Im}(f)=[0,\infty)$$
Podem observar que el domini pot ser un conjunt a elecció nostra (ja que podem escollir més petit o més gran) mentre que la imatge vindrà donada pel domini escollit.
De vegades, però, ens trobem que la nostra funció per certs motius no pot ser avaluada en certs punts ja que no està definida, així que haurem de excloure certs punts o intervals del domini.
Per exemple:
Si prenem la funció $$f(x)=\dfrac{x+1}{x}+1$$ podem veure que quan $$x = 0$$ tenim l'expressió $$\dfrac{1}{0}$$ i aquesta divisió no pot realitzar-se.
Per tant, el domini d'aquesta funció serà tots els reals excepte el zero:
$$\text{Dom}(f)=\mathbb{R}\setminus\{0\}=(-\infty,0)\cup(0,\infty)$$
I la imatge serà:
$$\text{Im}(f)=\mathbb{R}\setminus\{1\}=(-\infty,1)\cup(1,\infty)$$
Càlcul de dominis:
Per calcular el domini d'una funció hem de partir de que pot ser qualsevol nombre de la recta real ($$\mathbb{R}$$) i anar restringint el conjunt depenent de la funció. Per fer aquestes restriccions hem de localitzar els punts "febles" de les nostres funcions o millor dit, els punts de no definició. A continuació llistem els conjunts de no definició de les principals funcions:
| Funció | Conjunt de no definició |
| $$f(x)=\log(g(x))$$ | $$\{x \ | \ g(x) \leqslant 0 \} =$$ els valors de $$x$$ tal que $$g(x)$$ es fa negativa o zero |
| $$f(x)=\sqrt{g(x)}$$ | $$\{x \ | \ g(x) < 0 \}=$$ els valors de $$x$$ tal que $$g(x)$$ es fa negativa |
| $$f(x)=\dfrac{g(x)}{h(x)}$$ | $$\{x \ | \ h(x)=0 \}=$$ els valors de $$x$$ tal que $$h(x)$$ val zero |
| $$f(x)=\sqrt[2n]{g(x)}$$ | $$\{x \ | \ g(x) < 0 \}=$$ els valors de $$x$$ tal que $$g(x)$$ es fa negativa |
Si prenem la funció $$f(x)=\Big( \dfrac{2x+1}{x-4}-\ln(x+8)\Big)\cdot\sqrt{x^2+1}$$ i volem trobar el seu domini, hem de considerar que és tota la recta real i anar restringint segons trobem punts o intervals de no definició.
En aquest cas, observem que tenim 3 possibles intervals de no definició:
- quan $$x-4$$ sigui zero $$\Rightarrow x-4=0\Rightarrow x=4 \ $$ la funció no estarà definida.
- quan $$x+8$$ sigui negatiu o zero $$\Rightarrow x+4 \leqslant 0 \Rightarrow x\leqslant-8 \ $$ la funció no estarà definida.
- quan $$x^+1$$ sigui negatiu $$\Rightarrow x^2+1< 0 \Rightarrow x^2< -1 \ $$, cosa que no pot passar ja que $$x^2$$ sempre és positiu, per tant la funció no té intervals de no definició.
Llavors, podem concloure que el domini de la nostra funció serà: $$$ \text{Dom}(f)=(-8,4)\cup(4,\infty)$$$
Representació gràfica
Suposem que tenim una funció $$f(x)$$. Per representar-la gràficament hem de trobar primer el seu domini per saber en quins punts hem de avaluar-la.
Un cop trobat el domini procedirem a fer la representació. Com ho farem? Bé, la manera més simple i senzilla és mitjançant una taula de valors, és a dir, donarem valors a la variable $$x$$ i trobarem el valor de $$f(x)$$ i dibuixarem el punt trobat, $$(x,f(x))$$ en el pla usant les coordenades cartesianes.
Prenguem la funció $$f(x)=2x+1$$ i fem la taula de valors:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$f(2)=2\cdot(-2)+1=-3$$ |
| $$-1$$ | $$f(2)=2\cdot(-1)+1=-1$$ |
| $$0$$ | $$f(2)=2\cdot(0)+1=1$$ |
| $$1$$ | $$f(2)=2\cdot(1)+1=3$$ |
| $$2$$ | $$f(2)=2\cdot(2)+1=5$$ |
i per tant trobem els parells de punts:
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$-3$$ |
| $$-1$$ | $$-1$$ |
| $$0$$ | $$1$$ |
| $$1$$ | $$3$$ |
| $$2$$ | $$5$$ |
els dibuixarem en el pla $$XY$$ i els unirem amb una línia. Al final obtenim:
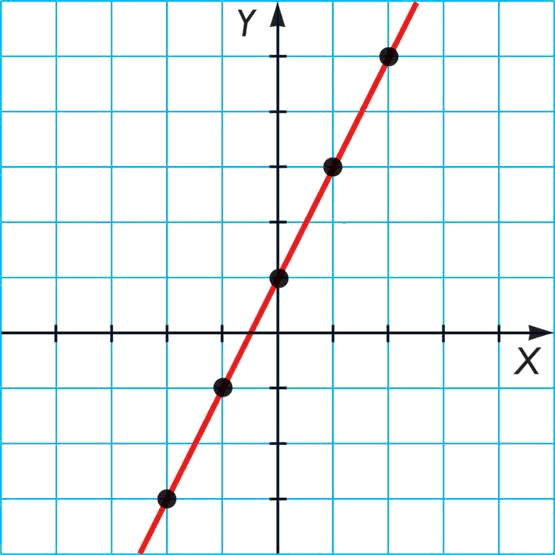
on hem marcat amb punts les coordenades trobades a la taula de valors.
Aquest procediment (fer la taula de valors) pot ser-nos molt útil quan hem de dibuixar una funció, però a vegades ens pot desconcertar, ja que hi ha funcions molt diverses i de vegades només trobant uns quants punts a la taula de valors no n'hi ha prou per poder dibuixar la funció.
