Concavidad y convexidad, puntos de inflexión de una función

Concavidad y convexidad

Se dice que una función $f (x)$ es convexa si al unir dos puntos cualesquiera de la gráfica, el segmento trazado queda por encima de la gráfica:

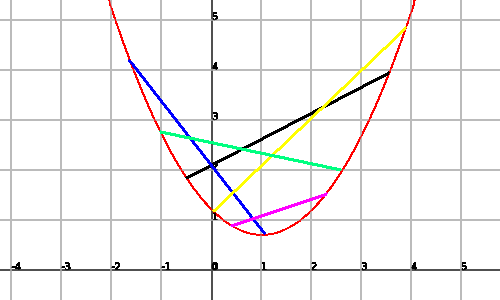
imagen

En esta imagen podemos observar con distintos colores diferentes segmentos que unen dos puntos de la gráfica y que quedan por encima de ella.

Ejemplo

Un ejemplo de función no convexa es: 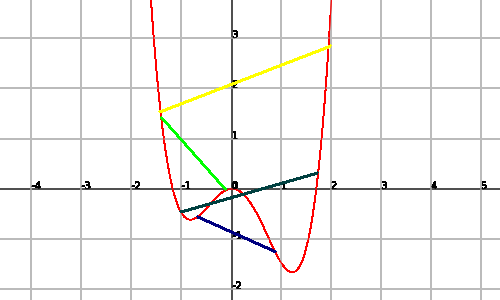imagen ya que encontramos segmentos que unen dos puntos de la gráfica y que pasan por debajo de ésta.

Por otro lado, se dice que una función $f (x)$ es cóncava si la función $- f (x)$ es convexa, es decir, si los segmentos que unen los puntos de la gráfica $f (x)$ están todos situados por debajo de la gráfica.

Ejemplo

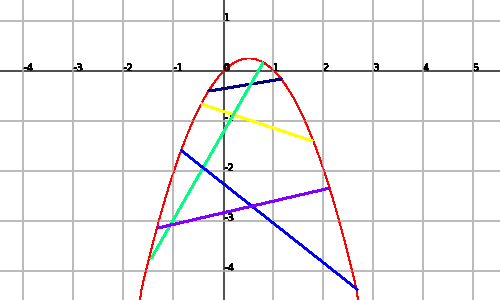
Veamos un ejemplo de función cóncava: imagen

Vulgarmente, podemos decir que las funciones convexas son funciones curvas que presentan primero un descenso y luego un ascenso y las funciones cóncavas funciona al revés, primero un ascenso y luego un descenso.

Las funciones, pero, pueden presentar partes cóncavas y partes convexas en una misma gráfica, por ejemplo, la función 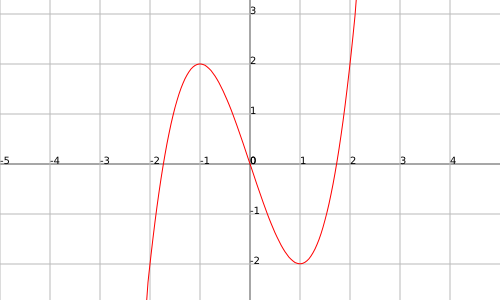$f (x) = (x + 1)^{3} - 3 (x + 1)^{2} + 2$ presenta concavidad en el intervalo $(- \infty, 0)$ y convexidad en el intervalo $(0, \infty)$ : imagen

El estudio de la concavidad y convexidad se realiza a través de los puntos de inflexión.

Puntos de inflexión

Se define un punto de inflexión como el punto en que la función pasa de ser convexa a cóncava o de cóncava a convexa.

Ejemplo

Podemos ver en el ejemplo anterior que en el punto $x = 0$ (en el origen de coordenadas) la función pasa de ser cóncava a ser convexa, por lo tanto decimos que $x = 0$ es punto de inflexión. imagen

Una característica de los puntos de inflexión es que son los puntos donde la función derivada tiene máximos y mínimos. Si nos fijamos, cuando nos acercamos a un punto de inflexion la función cada vez crece más (o decrece menos), pero al sobrepasar el punto de inflexión la función empieza a crecer menos (o decrecer menos). Esto significa que justamente donde haya un punto de inflexión la derivada tendrá un máximo o un mínimo. Consecuentemente encontraremos los puntos de inflexión buscando ceros de la segunda derivada.

Vamos a ilustrar el proceso con un ejemplo para así dar una explicación simple y clara:

Ejemplo

Consideraremos la función $f (x) = x^{3} - 3 x$ (es la función representada en la anterior gráfica).

Sabemos ya calcular los máximos y los mínimos de la función 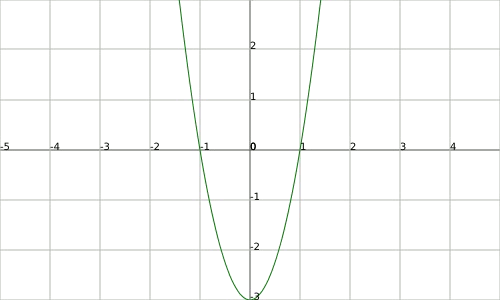$f (x)$ usando la primera derivada. La expresión de ésta es $f^{'} (x) = 3 x^{2} - 3$ y justamente encontramos máximos y mínimos respectivamente en $x = - 14$ y $x = 1$ . Si representamos la gráfica de la derivada tenemos: imagen

Observamos que justamente donde la derivada tiene un mínimo es donde la función tiene el punto de inflexión.

Para saber qué punto es vamos a derivar la función derivada e igualarla a cero: $f^{″} (x) = 6 x \Rightarrow 6 x = 0 \Rightarrow x = 0$ y por tanto la función original en $x = 0$ tiene un punto de inflexión.

El proceso para encontrar los puntos de inflexión, al igual que los máximos y mínimos, es un proceso algorítmico y muy mecánico. Derivar la función dos veces, igualar a cero y encontrar las soluciones de la ecuación. Estas soluciones justamente serán donde tengamos puntos de inflexión.