For the analysis of a function we also need to determine where the function is concave or convex. In other words, we need to determine the curvature of the function.
We say that a function $$f$$ is concave on an interval $$(a,b)$$ if for all $$x \in (a,b) f''(x)<0$$ . On the contrary, we say that a function $$f$$ is convex in an interval $$(a,b)$$ if for all $$x \in (a,b) f''(x)>0$$.
How do we find the intervals of concavity and convexity?
Study of the concavity of a function
- Find the second derivative of $$f(x)$$ and its roots
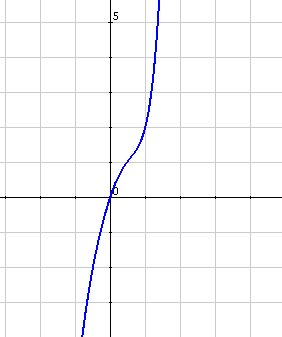
$$f(x)=3x^3-6x+1 \Rightarrow f'(x)=9x^2-6 \Rightarrow f''(x)=18x \\ f''(x)=18x=0 \Rightarrow x=0$$
- We separate by intervals limited by the zeros of the second derivative and any possible discontinuities of the function (if there are any)
In this case, there will be only two intervals separated at the zero.
- Let's take any value in each of the intervals and let's evaluate the second derivative, then:
$$f''(-1)=-18 <0 \Rightarrow$$ Concave
$$f''(1)= 18>0 \Rightarrow$$ Convex
Namely if in a point of the interval the second derivative is negative, the curvature is called concave; if in a point of an interval the second derivative is positive, the curvature is called convex.
- We determine the concavity in each of the intervals.
In our example, in the negative numbers, the function is concave, while it is convex in the positive numbers.
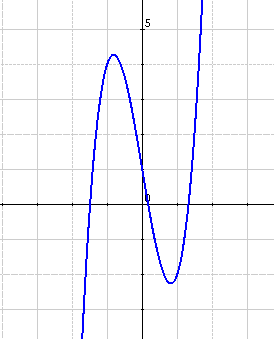
Let $$f(x)=x^5-2x^2+3x$$
- $$f''(x)=20x^3-4 \\ f''(x)=0 \Rightarrow x \approx 0.58$$
- There are two intervals: $$(- \infty, 0.58), \ (0.58, \infty)$$
- We chose any point of every interval:
$$f''(0)=-4 < 0 \Rightarrow$$ Concave
$$f''(1)=16 > 0 \Rightarrow $$ Convex
- Thus the result is
$$(-\infty, 0.58)$$ Concave
$$(0.58, \infty)$$ Convex