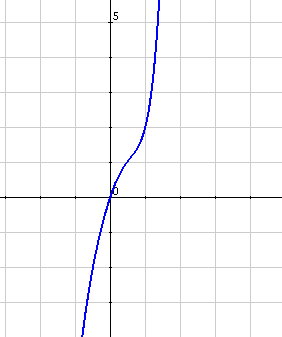
L'anàlisi d'una funció requereix també poder determinar la concavitat o convexitat per intervals. En altres paraules es tracta de determinar el tipus de curvatura de la funció.
Diem que una funció
Però, com podem trobar els intervals de concavitat i convexitat?
Estudi de la concavitat d'una funció
- Es troba la segona derivada de
- Separem per intervals limitats pels zeros de la segona derivada acabats de trobar i les discontinuïtats de la funció (si n'hi ha)
En aquest cas, hi haurà només dos intervals, separats en el zero. És a dir, els números negatius formen un interval i els positius altre.
- Es pren un valor qualsevol de cada interval i es determina la derivada segona en aquest valor:
És a dir, si en un punt de l'interval la derivada segona és negativa, la curvatura es diu còncava, i si en un punt d'un interval la derivada segona és positiva, la curvatura es diu convexa.
- Es dóna la concavitat dels intervals.
L' interval dels nombres negatius és còncau, mentre que el dels positius és convex.
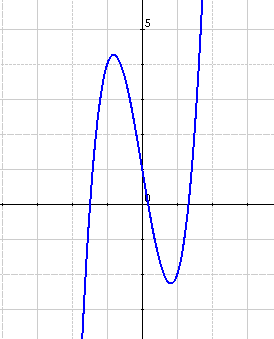
Exemple
Sigui
- Hi ha dos intervals:
- Es tria un punt qualsevol de cada interval:
- Es dóna el resultat