La idea de creixement o decreixement porta de la mà la idea d'interval o entorn. Doncs bé, una funció tindrà trossos, trams o intervals creixents i / o decreixents. Ara farem un estudi d'aquests intervals mitjançant l'ús de les derivades.
Sigui la funció
-
En primer lloc es calcula la derivada de
-
S'obtenen les arrels de la derivada. Per això, s'imposa
- S'estableixen intervals oberts amb les arrels trobades i les possibles discontinuïtats de la funció:
En aquest cas, els dos intervals (no hi ha discontinuïtats en
- Es tria un valor per a cada interval i es calcula el signe de la derivada. Vegeu de triar un valor en el primer interval implica triar un nombre qualsevol entre
Per al segon interval podem triar, per exemple, el
És a dir, ja es poden establir els intervals creixents i decreixents:
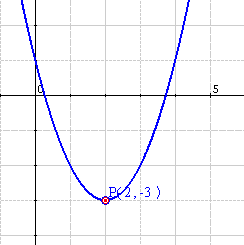
Exemple
Sigui ara la funció
Es calcula la derivada
Es calculen les arrels de la derivada,
Es construeixen els intervals a partir de les arrels i les discontinuïtats (en aquest cas hi ha discontinuïtat en
Els intervals queden doncs,
Es trien valors qualssevol per a cada un dels intervals i es calcula el valor de la derivada en aquests punts.
Interval 1:
Interval 2:
Interval 3:
Interval 4:
En resum, doncs,
