La idea de crecimiento o decrecimiento lleva de la mano la idea de intervalo o entorno. Una función tendrá trozos, tramos o intervalos crecientes y/o decrecientes. Ahora vamos a hacer un estudio de dichos intervalos mediante el uso de las derivadas.
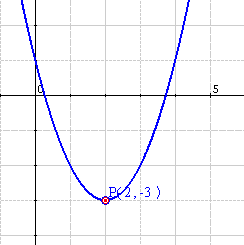
Sea nuestra función $$$f(x)=x^2-4x+1$$$ Queremos estudiar esta función, evaluando cuando ésta es creciente o decreciente, y para ello debemos determinar sus intervalos y estudiar sus derivadas. Para tal propósito es útil seguir los siguientes pasos:
-
En primer lugar se calcula la derivada de $$f(x)$$ $$$f'(x)=2x-4$$$
-
Se obtienen las raíces de la derivada. Para ello,se impone $$f'(x)=0$$: $$$f'(x)=2x-4=0 \Longrightarrow x=2$$$ La raíz es $$x=2$$.
- Se establecen intervalos abiertos con las raíces encontradas y las posibles discontinuidades de la función:
En este caso, los dos intervalos (no hay discontinuidades en $$f (x)$$) serán: $$(-\infty, 2) \cup (2,\infty)$$ (Donde el símbolo utilizado se lee 'unión'.)
- Se elige un valor para cada intervalo y se calcula el signo de la derivada. Véase que elegir un valor en el primer intervalo implica elegir un número cualquiera entre $$-\infty$$ y $$2$$:
$$f'(1)=2 \cdot 1-4=-2 < 0 $$, Decrecimiento
Para el segundo intervalo podemos elegir, por ejemplo, el $$10$$
$$f'(1)=2 \cdot 10 -4=16 >0$$, Crecimiento
Es decir, ya se pueden establecer los intervalos crecientes y decrecientes:
$$(-\infty , 2)$$ Decrecimiento
$$(2,\infty)$$ Crecimiento
Sea ahora la función $$$\displaystyle f(x)=\frac{x^4}{(x-2)^2}$$$ Se estudian sus intervalos:
Se calcula la derivada $$$\displaystyle f'(x)=\frac{4x^3(x-2)^2-x^4\cdot 2(x-2)}{(x-2)^4}=\frac{2x^3(x-4)}{(x-2)^3}$$$
Se calculan las raíces de la derivada, $$f '(x) =0$$ $$$ f'(x)=0 \Rightarrow \displaystyle \frac{2x^3(x-4)}{(x-2)^3}=0 \Rightarrow x=0 \mbox{ ó } x=4$$$
Se construyen los intervalos a partir de las raíces y las discontinuidades (en este caso hay discontinuidad en $$x=2$$).
Los intervalos quedan pues, $$(-\infty, 0) \cup (0,2) \cup (2,4) \cup (4,\infty)$$. La función se separa en cuatro intervalos.
Se eligen valores cualesquiera para cada uno de los intervalos y se calcula el valor de la derivada en esos puntos.
Intervalo 1: $$\displaystyle f'(-1)=-\frac{10}{27} < 0 \Rightarrow $$ Decreciente
Intervalo 2: $$f'(1)=6 > 0 \Rightarrow$$ Creciente
Intervalo 3: $$f'(3)=-54 < 0 \Rightarrow$$ Decreciente
Intervalo 4: $$\displaystyle f'(5)=\frac{250}{27}>0 \Rightarrow$$ Creciente
En resumen, pues, $$$\begin{array}{l} (-\infty, 0) \mbox{ Decreciente }\\ (0,2) \mbox{ Creciente }\\ (2,4) \mbox{ Decreciente } \\ (4, \infty) \mbox{ Creciente } \end{array}$$$
