Increasing and decreasing intervals

The idea of increasing or decreasing functions is related to having environments or intervals where the function is increasing or decreasing.

A function will have different parts, some of them increasing and/or decreasing. Now we will study these intervals using the derivatives.

Let's consider the following function $$$f(x)=x^2-4x+1$$$ We want to study this function, evaluating when is increasing or decreasing, and for that we must determine the intervals where the derivative is positive or negative. We can proceed in several steps:

  1. First of all we compute the derivative of $$f(x)$$ $$$f'(x)=2x-4$$$

  2. Then we find the roots of the derivative. For that, we impose $$f'(x)=0$$: $$$f'(x)=2x-4=0 \Longrightarrow x=2$$$ The root is $$x=2$$.

  3. We establish the intervals below and above the roots we have found, as well as any possible discontinuities:

In this case, we have two intervals (there are no discontinuities in $$f (x)$$):$$(-\infty, 2) \cup (2,\infty)$$ (Where the symbol we used is read as 'union').

  1. We chose a value belonging to each of the intervals and we determine whether the derivative is positive or negative. In our example we chose a numer between $$-\infty$$ and $$2$$:

$$f'(1)=2 \cdot 1-4=-2 < 0 $$, Decreasing

And a number greater than $$2$$, for example, $$10$$

$$f'(1)=2 \cdot 10 -4=16 >0$$, Increasing

Namely the increasing and decreasing intervals can be established:

$$(-\infty , 2)$$ Decreasing

$$(2,\infty)$$ Increasing

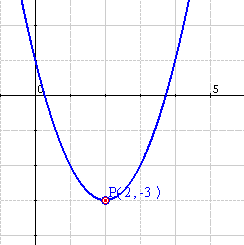
imagen

Let's consider now the function $$$\displaystyle f(x)=\frac{x^4}{(x-2)^2}$$$ And let's study its intervals:

The derivative is $$$\displaystyle f'(x)=\frac{4x^3(x-2)^2-x^4\cdot 2(x-2)}{(x-2)^4}=\frac{2x^3(x-4)}{(x-2)^3}$$$

The roots of the derivative, $$f '(x) =0$$ are $$$ f'(x)=0 \Rightarrow \displaystyle \frac{2x^3(x-4)}{(x-2)^3}=0 \Rightarrow x=0 \mbox{ or } x=4$$$

The intervals are constructed from the roots and the discontinuities (in this case there is discontinuity at $$x=2$$).

The intervals are then: $$(-\infty, 0) \cup (0,2) \cup (2,4) \cup (4,\infty)$$. The function has four intervals.

We chose values belonging to all of these intervals and we compute the value of its derivative:

Interval 1: $$\displaystyle f'(-1)=-\frac{10}{27} < 0 \Rightarrow $$ Decreasing

Interval 2: $$f'(1)=6 > 0 \Rightarrow$$ Increasing

Interval 3: $$f'(3)=-54 < 0 \Rightarrow$$ Decresing

Interval 4: $$\displaystyle f'(5)=\frac{250}{27}>0 \Rightarrow$$ Increasing

In short, then $$$\begin{array}{l} (-\infty, 0) \mbox{ Decresing }\\ (0,2) \mbox{ Increasing }\\ (2,4) \mbox{ Decreasing } \\ (4, \infty) \mbox{ Increasing } \end{array}$$$