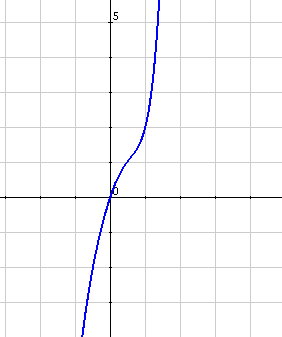
El análisis de una función requiere también poder determinar la concavidad o convexidad por intervalos. En otras palabras se trata de determinar el tipo de curvatura de la función.
Decimos que una función
Pero, ¿cómo podemos encontrar los intervalos de concavidad y convexidad?
Estudio de la concavidad de una función
- Se halla la segunda derivada de
- Separamos por intervalos limitados por los ceros de la segunda derivada acabados de encontrar y las discontinuidades de la función (si las hay)
En este caso, habrá solo dos intervalos, separados en el cero. Es decir, los números negativos forman un intervalo y los positivos otro.
- Se toma un valor cualquiera de cada intervalo y se determina la derivada segunda en ese valor:
Es decir, si en un punto del intervalo la derivada segunda es negativa, la curvatura se llama cóncava; si en un punto de un intervalo la derivada segunda es positiva, la curvatura se llama convexa.
- Se da la concavidad de los intervalos.
El intervalo de los números negativos es cóncavo, mientras que el de los positivos es convexo.
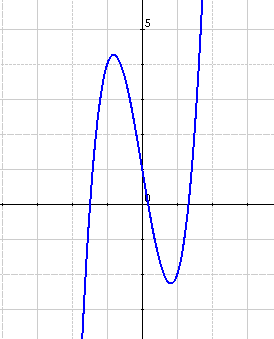
Ejemplo
Sea
- Hay dos intervalos:
- Se elige un punto cualquiera de cada intervalo:
- Se da el resultado