Optimización

Un espacio público tiene forma de triángulo rectángulo, cuyos lados miden $$4\ m$$ y $$12\ m$$ respectivamente. En este espacio público quiere construirse un parque infantil, pero la normativa dice que éste debe ser rectangular. ¿Cuál es el área máxima que tendrá el parque infantil? O, lo que es lo mismo, ¿cuál es el rectángulo más grande que podemos inscribir en un triángulo rectángulo de lados $$4\ m$$ y $$12\ m$$?

Paso 1: Comprensión del problema.

Acostumbra a ser útil un dibujo/esquema del problema.

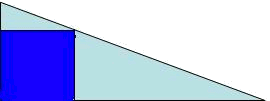
Paso 2: Construir la función.

Uno debe identificar la cantidad a maximizar o minimizar y saber escribirla matemáticamente. En este caso se pide maximizar el área del rectángulo. Así pues, si llamamos $$x$$ a la longitud e $$y$$ a la anchura, la función área $$A$$ será:

$$$A=x\cdot y$$$

Paso 3: Hallar ligaduras que permitan escribir la función área con una sola incógnita.

Puede utilizarse la semejanza de los triángulos (teorema de Tales).

$$$\dfrac{4-y}{x}=\dfrac{4}{12} \Rightarrow x=3(4-y)$$$

Paso 4: Reescribir la función, ahora de una sola variable.

Cambiamos el valor de $$x$$ por su dependencia de $$y$$, reescribiendo el valor de $$A=x\cdot y$$

$$$A(y)=3\cdot(4-y)\cdot y=-3y^2+12y$$$

Paso 5: Maximizar (o minimizar).

Se trata de igualar la derivada de la función a cero y obtener el valor de la variable.

$$$A'(y)=-6y+12=0 \Rightarrow y=2$$$

Paso 6: Hallar el valor de las otras variables involucradas.

La solución ha sido $$y=2\ m$$. Utilizamos que conocemos cómo depende $$x$$ de $$y$$ para hallar el valor de $$x$$

$$$\left.\begin{array}{c}x=3(4-y)\\y=2\end{array}\right\}\Rightarrow x=6\ m$$$

Paso 7: Dar el resultado.

El parque infantil más grande inscribible en este terreno tendrá unas dimensiones de $$6\times2$$ metros, que en total serán $$12\ m^2$$.

Determina la mínima distancia desde el punto $$(0,1)$$ hasta la parábola $$y=x^2$$.

Paso 1: Comprensión del problema.

Se trata de hallar la distancia entre una parábola centrada en el orígen de cordenadas $$(0,0)$$ y el punto $$(0,1)$$. Si uno quiere puede hacer el dibujo para mejor comprensión.

Pas 2: Construir la función.

Debemos minimizar la distancia, que llamaremos $$d$$.

La función distancia la construimos -usando el teorema de Pitágoras- entre los puntos $$(0,1)$$ y $$(x,y)$$ que es la cordenada de cualquiera de los puntos de la parábola.

Así pues,

$$$d^2=(0-x)^2+(1-y)^2\Rightarrow d=\sqrt{x^2+(1-y)^2}$$$

Paso 3:Hallar ligaduras que permitan escribir la función área con una sola incógnita.

En este caso sabemos directamente que $$y=x^2$$

Paso 4: Reescribir la función, ahora de una sola variable.

La función resulta $$d(x)=\sqrt{x^2+(1-x^2)^2}$$

Paso 5: Maximizar (o minimizar).

Se trata de igualar la derivada de la función a cero y obtener el valor de la variable.

$$$d'(x)=\dfrac{1}{2}\ \dfrac{\ 2x+2(1-x^2)(-2x)\ }{\sqrt{x^2+(1-x^2)^2}}=0$$$

Si seguimos con el cálculo,

$$$2x-4x(1-x^2)=0\Rightarrow \left\{ \begin{array}{cc}x=0\ , & \ \\x=\dfrac{\sqrt{2}}{2} & \ \ \ \mbox{or}\ \ \ \ x=-\dfrac{\sqrt{2}}{2}\end{array}\right.$$$

Paso 6: Hallar el valor de las otras variables involucradas.

Cada valor de $$x$$ tiene asociado un valor de $$y \ \ $$ ($$y=x^2$$)

$$$x=0\ \ \ \Rightarrow \ y=0$$$

$$$x=\dfrac{\sqrt{2}}{2}\ \Rightarrow \ y=\dfrac{1}{2}$$$

$$$x=-\dfrac{\sqrt{2}}{2}\ \Rightarrow y=\dfrac{1}{2}$$$

Paso 7: Dar el resultado.

En este caso hay tres puntos situados a la misma distancia, que es la mínima posible. Los tres puntos son:

$$$\left(-\dfrac{\sqrt{2}}{2},\dfrac{1}{2}\right)\ \ ;\ \ \left(0,0\right)\ \ ;\ \ \left(\dfrac{\sqrt{2}}{2},\dfrac{1}{2}\right)$$$

Para todos ellos $$d=1$$, lo cual es una comprobación de que efectivamente los tres puntos se encuentran a la misma distancia y de que no hay errores en los cálculos.