Optimització

Exemple

Un espai públic té forma de triangle rectangle, els costats del qual mesuren $4m$ i $12m$ respectivament. En aquest espai públic es vol construir un parc infantil, però la normativa diu que aquest ha de ser rectangular. Quin és l'àrea màxima que tindrà el parc infantil? O, el que és el mateix, quin és el rectangle més gran que podem inscriure en un triangle rectangle de costats $4m$ i $12m$?

Pas 1: Comprensió del problema.

Acostuma a ser útil fer-se un dibuix o esquema del problema.

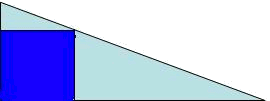
Pas 2: Construir la funció.

Un ha d'identificar la quantitat a maximitzar o minimitzar i saber escriure-la matemàticament. En aquest cas es demana maximitzar l'àrea del rectangle. Així doncs, si diem $x$ a la longitud i $y$ a l'amplada, la funció àrea $A$ serà:

$$A=x\cdot y$$

Pas 3: Trobar dependències que permetin escriure la funció àrea amb una sola incògnita.

Es pot utilitzar la semblança dels triangles (teorema de Tales).

$${\displaystyle \frac{4-y}{x}}={\displaystyle \frac{4}{12}}\Rightarrow x=3(4-y)$$

Pas 4: Reescriure la funció, ara d'una sola variable.

Canviem el valor de $x$ per la seva dependència de $y$, reescrivint el valor de $A=x\cdot y$

$$A(y)=3\cdot (4-y)\cdot y=-3y^2+12y$$

Pas 5: Maximitzar (o minimitzar).

Es tracta d'igualar la derivada de la funció a zero i obtenir el valor de la variable.

$$A^{\prime }(y)=-6y+12=0\Rightarrow y=2$$

Pas 6: Trobar el valor de les altres variables involucrades.

La solució ha estat $y=2m$. Utilitzem que coneixem com depèn $x$ de $y$ per trobar el valor de $x$

$$\begin{array}{c}x=3(4-y)\\ y=2\end{array}\}\Rightarrow x=6m$$

Pas 7: Donar el resultat.

El parc infantil més gran inscrit en aquest terreny tindrà unes dimensions de $6\times 2$ metres, que en total seran $12m^2$.

Exemple

Determina la mínima distància des del punt $(0,1)$ fins a la paràbola $y=x^2$.

Pas 1: Comprensió del problema.

Es tracta de trobar la distància entre una paràbola centrada en l'origen de coordenades $(0,0)$ i el punt $(0,1)$. Si un vol pot fer el dibuix per a una millor comprensió.

Pas 2: Construir la funció.

Hem de minimitzar la distància, que anomenarem $d$.

La funció distància la construïm -usant el teorema de Pitàgores- entre els punts $(0,1)$ i $(x,y)$ que és la coordenada de qualsevol dels punts de la paràbola.

Així doncs,

$$d^2=(0-x{)}^2+(1-y{)}^2\Rightarrow d=\sqrt{x^2+(1-y{)}^2}$$

Pas 3:Trobar dependències que permetin escriure la funció àrea amb una sola incògnita.

En aquest cas sabem directament que $y=x^2$

Pas 4: Reescriure la funció, ara d'una sola variable.

La funció resulta $d(x)=\sqrt{x^2+(1-x^2{)}^2}$

Pas 5: Maximitzar (o minimitzar).

Es tracta d'igualar la derivada de la funció a zero i obtenir el valor de la variable.

$$d^{\prime }(x)={\displaystyle \frac{1}{2}}{\displaystyle \frac{2x+2(1-x^2)(-2x)}{\sqrt{x^2+(1-x^2{)}^2}}}=0$$

Si seguim amb el càlcul,

$$2x-4x(1-x^2)=0\Rightarrow \{\begin{array}{cc}x=0,& \\ x={\displaystyle \frac{\sqrt{2}}{2}}& \text{or}x=-{\displaystyle \frac{\sqrt{2}}{2}}\end{array}$$

Pas 6: Trobar el valor de les altres variables involucrades.

Cada valor de $x$ té associat un valor de $y$ ($y=x^2$)

$$x=0\Rightarrow y=0$$

$$x={\displaystyle \frac{\sqrt{2}}{2}}\Rightarrow y={\displaystyle \frac{1}{2}}$$

$$x=-{\displaystyle \frac{\sqrt{2}}{2}}\Rightarrow y={\displaystyle \frac{1}{2}}$$

Pas 7: Donar el resultat.

En aquest cas hi ha tres punts situats en la mateixa distància, que és la mínima possible. Els tres punts són:

$$(-{\displaystyle \frac{\sqrt{2}}{2}},{\displaystyle \frac{1}{2}});(0,0);({\displaystyle \frac{\sqrt{2}}{2}},{\displaystyle \frac{1}{2}})$$

Per a tots ells $d=1$, amb el que es comprova que efectivament els tres punts es troben en la mateixa distància i que no hi ha errors en els càlculs.