La recta tangente a una curva es la que coincide con la curva en un punto y con la misma derivada, es decir, el mismo grado de variación.
El conocimiento de la recta tangente permitirá resolver problemas sencillos: en primer lugar, se podrán encontrar tangentes a cualquier función que se pueda derivar, en cualquier punto, como se observa en el primer ejemplo resuelto a continuación. En segundo lugar y como se puede ver en el segundo ejemplo, se puede utilizar como condición en problemas más complejos.
La recta $$y= m\cdot x +b$$ es tangente a la curva $$f(x)$$ si cumple los siguientes requisitos:
- Pasa por el punto de tangencia: $$(a,f(a))$$
- Tiene el mismo pendiente (mismo valor de la derivada) que la curva en el punto de tangencia: $$m=f'(a)$$
Entonces, se puede escribir la ecuación de la recta tangente de la siguiente forma:$$$y-f(a)=f'(a)\cdot (x-a)$$$
Nota: Siempre se encontraran tangentes a funciones polinómicas de orden superior a 1, o a funciones no polinómicas. La tangente a una recta sería la propia recta.
Además, la recta tangente puede tener interesantes aplicaciones geométricas. La siguiente gráfica posición-tiempo muestra la evolución de un atleta desde que empieza a correr. Se puede ver que el eje vertical representa la distancia recorrida, mientras que el horizontal representa el tiempo en segundos.
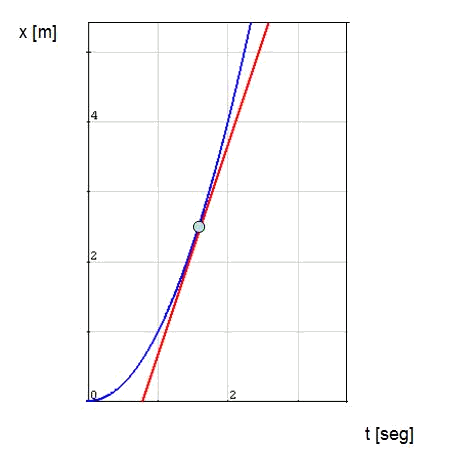
Teniendo en cuenta que la velocidad es la derivada de la posición respecto al tiempo, la pendiente de la parábola azul representa la velocidad instantánea.
Se puede ver que el corredor empieza con velocidad nula (parado) y va acelerando. La recta roja de la gráfica representa otro corredor que va a una velocidad constante y, en el instante marcado por el punto de tangencia, tiene la misma velocidad y se encuentra en el mismo punto.
El segundo corredor va más rápido que el primero hasta que es adelantado, y luego es el primero el que, gracias a que está acelerando, termina por delante.
Veamos algunos ejemplos:
Encuentre la recta tangente a $$f(x)=\sin x$$ en $$x=\pi$$.
a) Se buscan las coordenadas del punto de tangencia $$P$$: $$$\begin{array}{l} f(\pi)=0 \\ P=(\pi,0) \end{array}$$$
b) Se encuentra la derivada de $$f(x)$$ en $$x=\pi$$: $$$\begin{array}{l} f'(x)=\cos x \\ f'(\pi)= -1 \end{array}$$$
Tenemos ya el pendiente de la recta tangente.
Entonces, se escribe $$$\begin{array} {l} y-0=-1 \cdot (x -\pi) \\ y= \pi-x\end{array}$$$
Encontrar la ecuación de la recta tangente a la parábola $$f(x)=x^2-5x+6$$ y paralela a la recta $$3x+y-2=0$$
a) Se escribe la recta de la siguiente forma: $$$y=-3s+2$$$ Dado que la tangente que se quiere encontrar será paralela a esta recta, tendrá una pendiente $$m=-3$$
b) Sólo falta encontrar el punto de tangencia $$(a,f(a))$$, es decir, el punto en el que la parábola tendrá una derivada de valor $$m$$: $$$f'(x)=2x-5$$$ Y en el punto $$a$$, $$$\begin{array} {l} f'(a)=2a-5=-3 \\ a=1 \\ f(a)=2 \end{array}$$$ Finalmente, la ecuación de la recta tangente será: $$$\begin{array}{l}y-2=-3 \cdot (x-1) \\ y=-3x+5 \end{array}$$$
