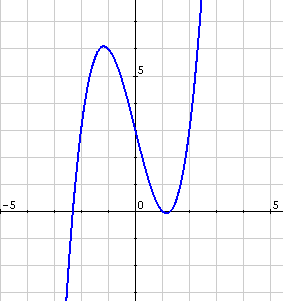
El análisis habitual de las funciones contiene el cálculo de sus máximos, mínimos y puntos de inflexión (a los máximos y mínimos les llamaremos genéricamente extremos relativos). ¿A qué nos referimos?
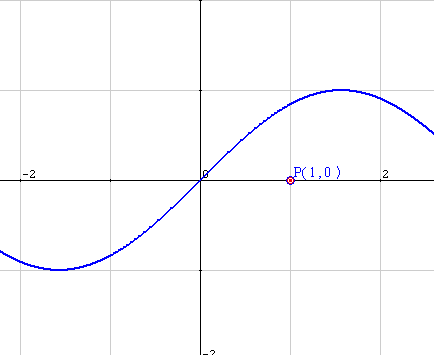
Efectivamente se observa un cambio de pendiente en algunos puntos, lo que se verá reflejado en ciertas propiedades significativas de las derivadas de la función. Véanse ahora las condiciones que definen los máximos, los mínimos y los puntos de inflexión utilizando el lenguaje matemático más formal.
Máximo relativo
Existe un máximo relativo en un punto $$a$$ si
- $$f '(a) = 0$$
- $$f ''(a) <0$$
Véase que la segunda derivada evaluada en el punto $$a$$ debe ser estrictamente menor que cero.
Mínimo relativo
Existe un mínimo relativo en un punto $$a$$ si
- $$f '(a) = 0$$
- $$f ''(a)>0$$
Véase en este caso, en cambio, que la segunda derivada de la función f evaluada en el punto 'a' debe se estrictamente positiva.
La existencia, pues, de un extremo relativo (máximo o mínimo) queda determinada por el valor nulo de la primera derivada y un valor no nulo de la segunda.
Punto de inflexión (o punto de silla)
Existe un punto de inflexión en un punto $$a$$ si
- $$\exists f '(a)$$ (léase: "existe $$f' (a)$$" o lo que es lo mismo, $$f (x)$$ es derivable en el punto $$a$$)
- $$f ''(a) = 0$$
Sea la función $$f(x)$$:$$$f(x)=x^3-4x+3$$$ El análisis de la función obliga a calcular los posibles extremos y puntos de de inflexión de dicha función. Deben seguirse los siguientes pasos.
Cálculo de los extremos relativos
-
Se deriva la función $$$f'(x)=3x^2-4$$$
-
Las raíces de la derivada nos dan los valores de $$x$$ dónde se hallarán los extremos de la función $$$\displaystyle f'(x)=3x^2-4=0 \Rightarrow x=\left\{\begin{array} f\Big(\frac{2}{\sqrt{3}}\Big)=\frac{2\sqrt{3}}{3} \\ -\frac{2\sqrt{3}}{3} \end{array}\right.$$$
-
Se calcula la segunda derivada y se evalúa en los punto encontrados: $$$\displaystyle f''(x)=6x \Rightarrow \left \{ \begin{array}{rl} f''\Big(\frac{2\sqrt{3}}{3}\Big)=4\sqrt{3} > 0 &\Rightarrow \mbox{ Mínimo } \\ f''\Big(\frac{-2\sqrt{3}}{3}\Big)=4\sqrt{3} < 0 &\Rightarrow \mbox{ Máximo }\end{array}\right.$$$
- Se dan las coordenadas de los puntos que son extremos. Para ello debe encontrarse el valor de $$f(x)$$ en los extremos. En el presente caso, $$$\displaystyle f(x)=x^3-4x+3 \Rightarrow \left\{\begin{array}{rl} f\Big(\frac{2 \sqrt{3}}{3} \Big)& \approx -0.08 \\ f\Big(-\frac{2\sqrt{3}}{3}\Big) &\approx 6.08\end{array}\right.$$$ Por lo tanto los extremos de la función son: Mínimo $$\displaystyle \Big(\frac{2\sqrt{3}}{3} , -0.08\Big)$$ Máximo $$\displaystyle \Big(-\frac{2\sqrt{3}}{3},6.08\Big)$$
Cálculo de los puntos de inflexión
- Se aprovecha el cálculo previo de la segunda derivada: $$f''(x)=6x$$
- Se buscan las raíces de la segunda derivada. En este caso, $$f''(x)=6x=0 \Rightarrow x=0$$
- Se sustituye dicho valor en la función $$f(x)$$ para hallar las coordenadas del punto de inflexión o punto de silla: $$f(0)=3$$
Y se concluye que el punto de inflexión es: $$(0, 3)$$