Màxims, mínims i punts d'inflexió d'una funció

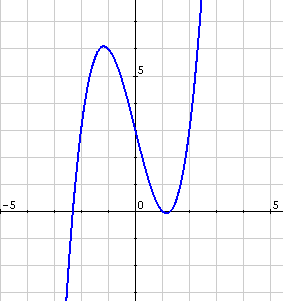
L'anàlisi habitual de les funcions conté el càlcul dels seus màxims, mínims i punts d'inflexió (als màxims i mínims els anomenarem genèricament extrems relatius). Però, a què ens referim?

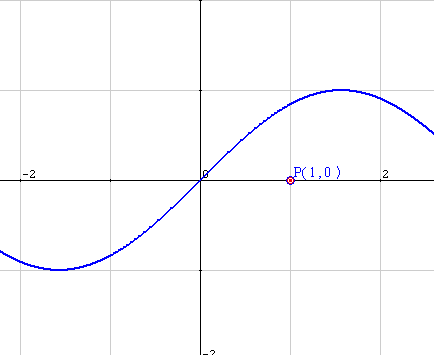
imagen

Efectivament s'observa un canvi de pendent en alguns punts, el que es veurà reflectit en certes propietats significatives de les derivades de la funció. Vegeu ara les condicions que defineixen els màxims, els mínims i els punts d'inflexió utilitzant el llenguatge matemàtic més formal.

Màxim relatiu

Hi ha un màxim relatiu en un punt $$a$$ si

  1. $$f '(a) = 0$$
  2. $$f ''(a) < 0$$

Vegeu que la segona derivada avaluada en el punt $$a$$ ha de ser estrictament menor que zero.

Mínim relatiu

Hi ha un mínim relatiu en un punt $$a$$ si

  1. $$f '(a) = 0$$
  2. $$f ''(a) > 0$$

Vegeu que en aquest cas, en canvi, la segona derivada de la funció $$f$$ avaluada en el punt $$a$$ ha de ser estrictament positiva.

L'existència, doncs, d'un extrem relatiu (màxim o mínim) queda determinada pel valor nul de la primera derivada i un valor no nul de la segona.

Punt d'inflexió (o punt de sella)

Hi ha un punt d'inflexió en un punt $$a$$ si

  1. $$\exists f '(a)$$ (es llegeix: "existeix $$f' (a)$$" o el que és el mateix, $$f (x)$$ és derivable en el punt $$a$$)
  2. $$f ''(a) = 0$$

Sigui la funció $$f(x)$$:$$$f(x)=x^3-4x+3$$$ L'anàlisi de la funció obliga a calcular els possibles extrems i punts d'inflexió d'aquesta funció. Cal seguir els següents passos:

Càlcul dels extrems relatius

  1. Es deriva la funció $$$f'(x)=3x^2-4$$$

  2. Les arrels de la derivada ens donen els valors de $$x$$ on es trobaran els extrems de la funció $$$\displaystyle f'(x)=3x^2-4=0 \Rightarrow x=\left\{\begin{array} f\Big(\frac{2}{\sqrt{3}}\Big)=\frac{2\sqrt{3}}{3} \\ -\frac{2\sqrt{3}}{3} \end{array}\right.$$$

  3. Es calcula la segona derivada i s'avalua en els punt trobats: $$$\displaystyle f''(x)=6x \Rightarrow \left \{ \begin{array}{rl} f''\Big(\frac{2\sqrt{3}}{3}\Big)=4\sqrt{3} > 0 &\Rightarrow \mbox{ Mínim } \\ f''\Big(\frac{-2\sqrt{3}}{3}\Big)=4\sqrt{3} < 0 &\Rightarrow \mbox{ Màxim }\end{array}\right.$$$

  4. Es donen les coordenades dels punts que són extrems. Per a això ha de trobar el valor de $$f (x)$$ en els extrems. En aquest cas, $$$\displaystyle f(x)=x^3-4x+3 \Rightarrow \left\{\begin{array}{rl} f\Big(\frac{2 \sqrt{3}}{3} \Big)& \approx -0.08 \\ f\Big(-\frac{2\sqrt{3}}{3}\Big) &\approx 6.08\end{array}\right.$$$ Per tant els extrems de la funció són: Mínim $$\displaystyle \Big(\frac{2\sqrt{3}}{3} , -0.08\Big)$$ Màxim $$\displaystyle \Big(-\frac{2\sqrt{3}}{3},6.08\Big)$$

Càlcul dels punts d'inflexió

  1. S'aprofita el càlcul previ de la segona derivada: $$f''(x)=6x$$
  2. Es busquen les arrels de la segona derivada. En aquest cas, $$f''(x)=6x=0 \Rightarrow x=0$$
  3. Es substitueix aquest valor en la funció $$f(x)$$ per trobar les coordenades del punt d'inflexió o punt de sella: $$f(0)=3$$

I es conclou que el punt d'inflexió és: $$(0, 3)$$

imagen