Definition and general term of a sequence

A sequence is a sorted and infinite collection of real numbers. Small letters usually denote the sequences.

Example

Here are some sequences: $a : 1, \sqrt{2}, - \frac{1}{3}, 0.27, \sqrt{7}, \dots$ $b : 1, 3, 9, 27, 81, \dots$ $c : \frac{1}{\sqrt{2}}, \frac{2}{\sqrt{2}}, \frac{3}{\sqrt{2}}, \frac{4}{\sqrt{2}}, \frac{5}{\sqrt{2}}, \dots$ $d : \frac{2}{3}, - \frac{3}{4}, \frac{4}{5}, - \frac{5}{6}, \frac{6}{7}, \dots$

To give a sorted list of numbers is to determine which is the first one, the second one, the third one... or in mathematical terms, it means to associate every natural number one and only one real number; that is, a sequence is an application of the set of natural numbers to the set of real numbers: $a : N \to R$ .

Example

The previous sequences are written:

$a : N \to R$

$1 \to 1$

$2 \to \sqrt{2}$

$3 \to - \frac{1}{3}$

$4 \to 0.27$

$5 \to \sqrt{7}$

$\dots$

$b : N \to R$

$1 \to 1$

$2 \to 3$

$3 \to 9$

$4 \to 27$

$5 \to 81$

$\dots$

The numbers that form the sequence are called terms, and we usually refer to them using the letter that names the sequence with a subscript that indicates the position the above mentioned term occupies in the sequence:

$a : N \to R$

$1 \to a_{1}$

$2 \to a_{2}$

$3 \to a_{3}$

$\dots$

$n \to a_{n}$

$\dots$

The symbol $a_{1}$ represents the first term of the sequence $a$ , $a_{2}$ is the second one, $a_{3}$ the third one, and so on; the symbol $a_{n}$ represents the term that occupies the position $n$ , this is the $n$ -th term of the sequence.

Example

Using the previous examples, we have

$a_{3}$ is the third term of the sequence $a$ , that is, $a_{3} = - \frac{1}{3} .$

$b_{5}$ is the fifth term of the sequence $b$ , that is, $b_{5} = 243.$

$c_{1}$ is the first term of the sequence $c$ , that is, $c_{1} = \frac{1}{\sqrt{2}} .$

$d_{4}$ is the fourth term of the sequence $d$ , that is, $d_{4} = - \frac{5}{6} .$

General term of a sequence

If the terms of a sequence follow a certain law in its formation, that is, if it is possible to give a formula that relates the value of the $n$ -th term to the natural number $n$ , we will call such formula the general term of the sequence.

We can also interpret the general term as a real function, and then the sequence is interpreted as the values which the function takes in the natural numbers.

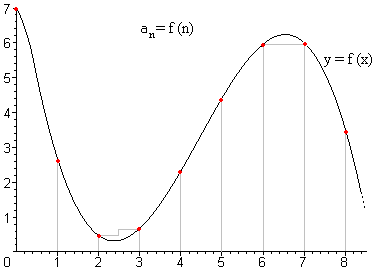
imagen

Example

In the sequence $a$ , the terms do not follow any rule or pattern in its formation, therefore it is not possible to give a general term.

In the sequence $c$ we see that all the terms are divided by $\sqrt{2}$ , and the numerator always coincides with its position, that is, the first term of the sequence has a number $1$ in the numerator, the second one has a number $2$ , the third one has a number $3$ , and so on; therefore, the $n$ -th term will take $n$ as a numerator, so the general term of such a sequence will be: $c_{n} = \frac{n}{\sqrt{2}} .$ As we have commented, the sequence $c$ corresponds to the taking the values of the natural numbers in the function $f (x) = \frac{x}{\sqrt{2}}$ .

To notice that the sequence is an application of the set of natural numbers, that is $n \in N$ , sometimes it is written as $(a_{n})_{n \in N}$ when it refers to the general term of the sequence.

Sequences recursively defined

Sometimes, when calculating the n-th term of a sequence, it is easier from the previous term, or terms than from the position it takes. In this case, although we are not giving the general term of the sequence, it is accepted as its definition, and it is said that the sequence is defined recursively. In these occasions, in addition to giving the formula that defines the sequence, it is necessary to give the first, or the first terms.

Example

In the sequence $b$ of the previous examples, we can observe that every term is the result of multiplying the previous one by $3$ : $a_{1} = 3$ $a_{2} = 3 \cdot a_{1} = 3 \cdot 3 = 9$ $a_{3} = 3 \cdot a_{2} = 3 \cdot 9 = 27$ $\dots$

so we may also define the sequence as $a_{1} = 3$ $a_{n} = 3 \cdot a_{n - 1}$

Example

Let's see another example where we verify that to define the sequence not always the previous term only is needed. We define the sequence in the following way; $a_{1} = 0; a_{2} = 1$ $a_{n} = a_{n - 1} + a_{n - 2}$

This sequence is called a Fibonacci sequence. This sequence has numerous mathematical properties but it was, curiously, presented through a study on the reproduction rates of rabbits.