Definició i terme general d'una successió

Una successió és una col·lecció ordenada i infinita de nombres reals. Se solen utilitzar lletres minúscules per denotar la successions.

Exemple

Són successions: $a : 1, \sqrt{2}, - \frac{1}{3}, 0.27, \sqrt{7}, \dots$ $b : 1, 3, 9, 27, 81, \dots$ $c : \frac{1}{\sqrt{2}}, \frac{2}{\sqrt{2}}, \frac{3}{\sqrt{2}}, \frac{4}{\sqrt{2}}, \frac{5}{\sqrt{2}}, \dots$ $d : \frac{2}{3}, - \frac{3}{4}, \frac{4}{5}, - \frac{5}{6}, \frac{6}{7}, \dots$

Donar una llista de números en ordre és determinar quin és el primer, el segon, el tercer, ... o en termes matemàtics, és associar a cada nombre natural un únic nombre real, és a dir, una successió és una aplicació del conjunt de nombres naturals al conjunt de nombres reals: $a : N \to R$ .

Exemple

La successions anteriors s'escriuen:

$a : N \to R$

$1 \to 1$

$2 \to \sqrt{2}$

$3 \to - \frac{1}{3}$

$4 \to 0.27$

$5 \to \sqrt{7}$

$\dots$

$b : N \to R$

$1 \to 1$

$2 \to 3$

$3 \to 9$

$4 \to 27$

$5 \to 81$

$\dots$

Els números que formen la successió els anomenem termes, i solem referir-nos a ells utilitzant la lletra que denota la successió amb un subíndex que ens indica quina posició ocupa aquest terme en la successió:

$a : N \to R$

$1 \to a_{1}$

$2 \to a_{2}$

$3 \to a_{3}$

$\dots$

$n \to a_{n}$

$\dots$

El símbol $a_{1}$ representa el primer terme de la successió $a$ , $a_{2}$ és el segon, $a_{3}$ el tercer, i així successivament; el símbol $a_{n}$ representa el terme que ocupa la posició $n$ , és a dir, l' $n$ -èsim terme de la successió.

Exemple

Utilitzant els exemples anteriors, tenim que

$a_{3}$ és el tercer terme de la successió $a$ , és a dir, $a_{3} = - \frac{1}{3} .$

$b_{5}$ és el cinquè terme de la successió $b$ , és a dir, $b_{5} = 243.$

$c_{1}$ és el primer terme de la successió $c$ , és a dir, $c_{1} = \frac{1}{\sqrt{2}} .$

$d_{4}$ és el quart terme de la successió $d$ , és a dir, $d_{4} = - \frac{5}{6} .$

Terme general d'una successió

Si els termes d'una successió segueixen una determinada llei en la seva formació, és a dir, si és possible donar una fórmula que relacioni el valor del terme $n$ -èsim amb un nombre natural , anomenarem a aquesta fórmula terme general de la successió.

També podem interpretar el terme general com una funció real, i aleshores interpretar la successió com els valors que pren la funció en els nombres naturals.

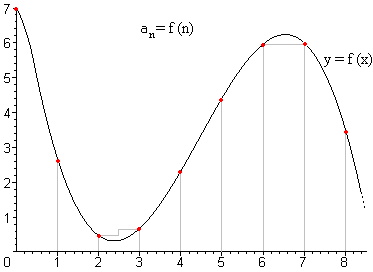
imagen

Exemple

En la successió $a$ , els termes no segueixen cap pauta o regla en la seva formació, de manera que no es pot donar un terme general.

En la successió $c$ veiem que tots els termes estan dividits per $\sqrt{2}$ , i el numerador coincideix sempre amb la posició que ocupa, és a dir, el primer terme de la successió té un $1$ en el numerador, el segon té un $2$ , el tercer té un $3$ , i així successivament, de manera que l' $n$ -èsim terme tindrà per numerador $n$ , així doncs, el terme general d'aquesta successió serà: $c_{n} = \frac{n}{\sqrt{2}} .$ Com hem comentat, la successió $c$ correspon a prendre els valors en els nombres naturals de la funció $f (x) = \frac{x}{\sqrt{2}}$ .

Per remarcar que la successió és una aplicació del conjunt de nombres naturals, és a dir que $n \in N$ , algunes vegades s'escriu $(a_{n})_{n \in N}$ quan es refereix al terme general de la successió.

Successions definides per recurrència

Hi ha ocasions en què calcular el terme $n$ -èsim és més fàcil a partir del terme, o termes, anteriors que de la posició que ocupa. En aquest cas, encara que no estem donant el terme general de la successió, s'accepta com a definició d'aquesta, i es diu que la successió està definida recursivament. En aquestes ocasions, a més de donar la fórmula que defineix la successió, cal donar el primer, o primers, termes.

Exemple

En la successió $b$ dels exemples anteriors, s'observa que cada terme és el resultat de multiplicar l'anterior per $3$ : $a_{1} = 3$ $a_{2} = 3 \cdot a_{1} = 3 \cdot 3 = 9$ $a_{3} = 3 \cdot a_{2} = 3 \cdot 9 = 27$ $\dots$

de tal manera que podríem definir la successió com: $a_{1} = 3$ $a_{n} = 3 \cdot a_{n - 1}$

Exemple

Vegem un altre exemple on comprovem que per definir la successió no sempre és necessari només el terme anterior.

Definim la successió de la següent manera; $a_{1} = 0; a_{2} = 1$ $a_{n} = a_{n - 1} + a_{n - 2}$

Aquesta successió s'anomena successió de Fibonacci . Aquesta successió té nombroses propietats matemàtiques però va ser, curiosament, presentada a través d'un estudi sobre la taxa de reproducció dels conills.