Definición y término general de una sucesión

Una sucesión es una colección ordenada e infinita de números reales. Se suelen utilizar letras minúsculas para denotar la sucesiones.

Ejemplo

Son sucesiones: $a : 1, \sqrt{2}, - \frac{1}{3}, 0.27, \sqrt{7}, \dots$ $b : 1, 3, 9, 27, 81, \dots$ $c : \frac{1}{\sqrt{2}}, \frac{2}{\sqrt{2}}, \frac{3}{\sqrt{2}}, \frac{4}{\sqrt{2}}, \frac{5}{\sqrt{2}}, \dots$ $d : \frac{2}{3}, - \frac{3}{4}, \frac{4}{5}, - \frac{5}{6}, \frac{6}{7}, \dots$

Dar una lista de números en orden es determinar cual es el primero, el segundo, el tercero,... o en términos matemáticos, es asociar a cada número natural un único número real, es decir, una sucesión es una aplicación del conjunto de números naturales al conjunto de números reales: $a : N \to R$ .

Ejemplo

La sucesiones anteriores se escriben:

$a : N \to R$

$1 \to 1$

$2 \to \sqrt{2}$

$3 \to - \frac{1}{3}$

$4 \to 0.27$

$5 \to \sqrt{7}$

$\dots$

$b : N \to R$

$1 \to 1$

$2 \to 3$

$3 \to 9$

$4 \to 27$

$5 \to 81$

$\dots$

Los números que forman la sucesión los llamamos términos, y solemos referirnos a ellos utilizando la letra que denomina la sucesión con un subíndice que nos indica que posición ocupa dicho término en la sucesión:

$a : N \to R$

$1 \to a_{1}$

$2 \to a_{2}$

$3 \to a_{3}$

$\dots$

$n \to a_{n}$

$\dots$

El símbolo $a_{1}$ representa el primer término de la sucesión $a$ , el $a_{2}$ es el segundo, $a_{3}$ el tercero, y así sucesivamente; el símbolo $a_{n}$ representa el término que ocupa la posición $n$ , es decir el $n$ -ésimo término de la sucesión.

Ejemplo

Utilizando los ejemplos anteriores, tenemos que

$a_{3}$ es el tercer término de la sucesión $a$ , es decir, $a_{3} = - \frac{1}{3} .$

$b_{5}$ es el quinto término de la sucesión $b$ , es decir, $b_{5} = 243.$

$c_{1}$ es el primer término de la sucesión $c$ , es decir, $c_{1} = \frac{1}{\sqrt{2}} .$

$d_{4}$ es el cuarto término de la sucesión $d$ , es decir, $d_{4} = - \frac{5}{6} .$

Término general de una sucesión

Si los términos de una sucesión siguen una determinada ley en su formación, es decir, si es posible dar una fórmula que relacione el valor del término $n$ -ésimo con el número natural $n$ , llamaremos a dicha fórmula término general de la sucesión.

También podemos interpretar el término general como una función real $f (x)$ . Y la sucesión se interpreta como los valores que toma la función en los números naturales.

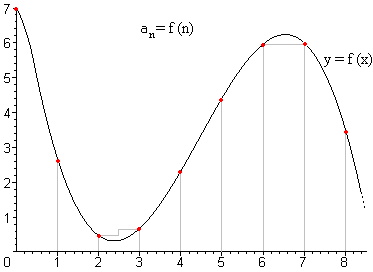
imagen

Ejemplo

En la sucesión $a$ , los términos no siguen ninguna pauta o regla en su formación, por lo que no se puede dar un término general.

En la sucesión $c$ vemos que todos los términos están divididos por $\sqrt{2}$ , y el numerador coincide siempre con la posición que ocupa, es decir, el primer término de la sucesión tiene un $1$ en el numerador, el segundo tiene un $2$ , el tercero tiene un $3$ , y así sucesivamente, con lo que el $n$ -ésimo término tendrá por numerador $n$ ; así pues, el término general de dicha sucesión será: $c_{n} = \frac{n}{\sqrt{2}} .$ Como hemos comentado, la sucesión $c$ corresponde a tomar los valores en los números naturales de la función $f (x) = \frac{x}{\sqrt{2}}$ .

Para remarcar que la sucesión es una aplicación del conjunto de números naturales, es decir que $n \in N$ , algunas veces se escribe $(a_{n})_{n \in N}$ cuando se refiere al término general de la sucesión.

Sucesiones definidas por recursión

Hay ocasiones en que calcular el término $n$ -ésimo es más fácil a partir del término, o términos, anteriores que de la posición que ocupa. En este caso, aunque no estamos dando el término general de la sucesión, se acepta como definición de esta, y se dice que la sucesión está definida recursivamente. En estas ocasiones, además de dar la fórmula que define la sucesión, es preciso dar el primer, o primeros, términos.

Ejemplo

En la sucesión $b$ de los ejemplos anteriores, se observa que cada término es el resultado de multiplicar el anterior por $3$ : $a_{1} = 3$ $a_{2} = 3 \cdot a_{1} = 3 \cdot 3 = 9$ $a_{3} = 3 \cdot a_{2} = 3 \cdot 9 = 27$ $\dots$

de tal forma que podríamos definir la sucesión como $a_{1} = 3$ $a_{n} = 3 \cdot a_{n - 1}$

Ejemplo

Veamos otro ejemplo donde comprobamos que para definir la sucesión no siempre es necesario solo el término anterior. Definimos la sucesión de la siguiente manera; $a_{1} = 0; a_{2} = 1$ $a_{n} = a_{n - 1} + a_{n - 2}$

Esta sucesión se denomina sucesión de Fibonacci. Esta sucesión tiene numerosas propiedades matemáticas pero fue, curiosamente, presentada a través de un estudio sobre la tasa de reproducción de los conejos.