Elements of a square root
When we solve the square root with this method we have to know the parts into which the square root is divided while proceeding. The components parts are:
- Radical, is the symbol that indicates that it is a square root.
- Radicand, is the number which square root we are calculating.
- Root, it is the very square root of the radicand.
- Auxiliary lines, they will help us solve the square root.
- Remainder, is the final number of the process to solve the square root.
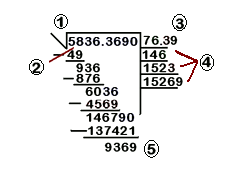
Calculation of the square root step by step
When the square root of a number is calculated it is necessary to realize that the result cannot be a natural number, but a decimal number. We will study the calculation of the square roots in which the solutions are natural numbers.
To calculate the square root of a number with several decimal digits we proceed this way:
-
The number is divided into groups of two numbers, starting from the right.
-
Calculate the number that, when multiplied by himself, is closest to, but does not exceed, the first group of numbers on the left. This way, the first number of the root is obtained and we place it on the right of the radicand, on the first auxiliary line. Then the square of this number is reduced from the first group.
-
On the right side of the remainder the second group is written and the number on the right is separated.
-
The number that is on the left side of the separated number is divided by the double of the obtained root. The quotient is written on the right of the divisor and the entire part of the number that results from the division is multiplied by the same quotient. If this product can be reduced from the dividend followed by the separated number, the quotient is the number of the root; otherwise, try with a lower number.
- Steps
Example
For example, let’s try it first with a number that is a perfect square:
Let's calculate the root of
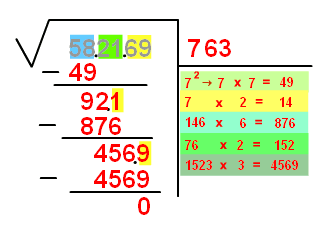
Step by step it would be:
1) We group in
| 58.21.69 |
2) We look for a number that risen up to
| 58.21.69 | 7 |
| 7·7=49 |
3) This result is reduced from
| 58.21.69 | 7 |
| -49 | 7·7=49 |
| 92.1 |
4) We write the double of
In this case
We make the subtraction, move down the next two digits and separate the last one (now
| 58.21.69 | 76 |
| -49 | 7·7=49 |
| 92.1 | 7·2=14 |
| -876 | 146·6=876 |
| 456.9 |
5) We do the same as in the previous step. Namely, we multiply
When we do the subtraction it comes to zero and, therefore, it is not necessary to continue.
We write
| 58.21.69 | 763 |
| -49 | 7·7=49 |
| 92.1 | 7·2=14 |
| -876 | 146·6=876 |
| 456.9 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 0 |
The square root of
Let's see now an example of a number that is not a perfect square, but a decimal number:
Example
The root of
1) the number of the radicand is divided in groups of two digits. The separation is done from the decimal sign (if there is one) from right to left.
If on the side of the decimals there is not an even number of digits, it is clear that a digit will be alone: in such a case, we add a zero.
If in the integer’s side we had left a number alone, it would remain like that. In our case we must add a zero next to
| 58.36,36.90 |
2) We look for a number that, multiplied by itself, is
In this case the number would be
| 58.36,36.90 | 7 |
| 7·7=49 |
3) We subtract
| 58.36,36.90 | 7 |
| -49 | 7·7=49 |
| 93.6 |
4) We write the double of
We subtract, move down the next two digits and separate the last one. In this case we move down
Since these are on the right side of the decimal point, in the first line (where we are writing) we put a decimal point as well. We will write:
| 58.36,36.90 | 76, |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 |
5) Now, we repeat the previous step. We multiply
The operation to be done is
We move down the following two digits. We write 3 in the first line. This is written as:
| 58.36,36.90 | 76,3 |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 1467.90 |
6) The same previous step is repeated. We multiply the root that we have written by now
The result is written on the following auxiliary line, and the first four numbers of the remainder
We write
| 58.36,36.90 | 76,3 |
| -49 | 7·7=49 |
| 93.6 | 7·2=14 |
| -876 | 146·6=876 |
| 603.6 | 76·2=152 |
| -4569 | 1523·3=4569 |
| 1467.90 | 763·2=1526 |
| -137421 | 15269·9=137421 |
| 9369 |
At this point, we can say that approximately the square root of
This operation, used as an example, is not finished. If we continue it would give

