Elements de l'arrel quadrada i algoritme de càlcul

Exemple

Fem aquest procediment primer amb un nombre que sigui un quadrat perfecte.

Busquem l'arrel de $582.169$ que és $763$ ja que $763\cdot 763=582.169$.

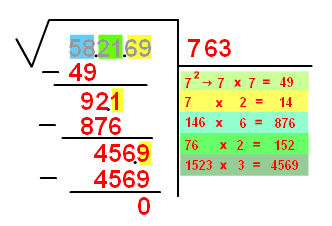
Pas a pas, seria:

1) Es separen de $2$ en $2$ les xifres del nombre $582169$, és a dir: $582169$. Ho escriurem així:

2) Es busca un nombre que elevat al quadrat doni proper a $58$, en aquest cas el nombre és $7$ donat que $7\cdot 7=49$. Ho escriurem:

3) Es resta aquest resultat de $58$ i per tant queda: $58-49=9$. Es baixen les dues xifres següents que són $21$. I es separa l'última xifra que és $1$. Ho escriurem:

4) Posem el doble de $7$ (és a dir $14$) en la tercera línia auxiliar i es divideix el nombre que queda a l'esquerra de la xifra separada (que era $1$) entre $14$.

En aquest cas, $92:14$ que dóna el nombre enter $6$ com a més proper. (Posem el $6$ al costat del $7$ de la primera línia.)

Restem, baixem les següents dues xifres i separem la última (ara un $9$). Escrit serà:

5) Fem el mateix que en el pas anterior. És a dir, multipliquem $76$ per dos (fem el doble) i es divideix el $456$ entre aquest doble (que és $152$) i que dóna $3$.

Quan es resten dóna zero i per tant no cal seguir.

Posem el $3$ en el primer línea, i ja s'ha trobat l'arrel buscada: $763$.

L'arrel quadrada de $582.169$ és $763$.

Exemple

L'arrel de $5836,369$

1) Es separa el número del radicand en grups de dues xifres. La separació es fa des del signe de decimal (si n'hi ha) cap a la dreta i cap a l'esquerra.

Si en el costat dels decimals no hi ha un nombre parell de xifres, és evident que queda una sola: en aquest cas, li afegim un zero.

Si en el costat dels enters ens quedés un nombre sol, es quedaria així. En el nostre cas hem d'afegir un zero al costat del $9$. Escrit serà:

2) Busquem un nombre que multiplicat per si mateix doni com a resultat el nombre que coincideixi o que més s'aproximi per sota a $58$. El resultat no pot ser més gran que $58$.

En aquest cas el nombre seria el $7$, perquè $7\cdot 7=49$. Ho escrivim:

3) Restem $49$ al primer grup de dues xifres de l'arrel, que ens dóna $9$. Baixem les següents $2$ xifres, és a dir $36$. Ara separem la darrera xifra, el $6$. Ho escrivim:

4) Posem el doble de $7$ (és a dir $14$) en la tercera línea auxiliar, i es divideix el nombre que queda a l'esquerra de la xifra separada (que era $6$) entre $14$. En aquest cas és $93:14$ que dóna el nombre enter $6$ com a més pròxim. (Posem el $6$ al costat del $7$ de la primera línia.)

Restem, baixem les dues xifres i separem l'última. En aquest cas, baixem $36$.

Com que aquestes estan a la dreta del punt decimal, a la primera línia, on anem escrivint l'arrel quadrada se li posa un punt decimal també. Ho escrivim:

5) Ara, fem el mateix que en el pas anterior. És a dir, multipliquem $76$ per dos (fem el doble) i es divideix el $603$ entre aquest doble (que és $152$) i que dóna $3,9$ pel que prenent la part entera, és $3$.

L'operació a realitzar per tant és $1523\cdot 3$, escrivim el resultat sota de l'últim resta que teníem i fem la diferència.

Baixem després les dues xifres. També posem el $3$ en la primera línia. Ho escrivim:

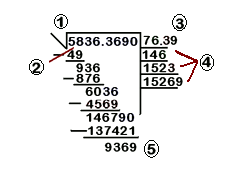
6) Tornem a fer el mateix. Multipliquem l'arrel que tenim escrita de moment $(76,3)$ per $2$ però ignorant el punt decimal, és a dir $763\cdot 2=1526$.

El resultat s'afegeix a la següent línea auxiliar, i es tornen a dividir els primers quatre números del residu $(1467)$ entre el resultat de la multiplicació i s'obté el número $9$ com a primera xifra que no és zero de la divisió.

El nou es posa en la línea de l'arrel i es multiplica $9$ per $15269$, el que dóna $137421$ que és la xifra que hem de restar a l'últim resta que era $146790$ que dóna $9369$.

En aquest moment, podem escriure que aproximadament tenim que l'arrel quadrada de $5836,369$ és $76,39$ amb un residu de $9369$.