Equation of the horizontal hyperbolas

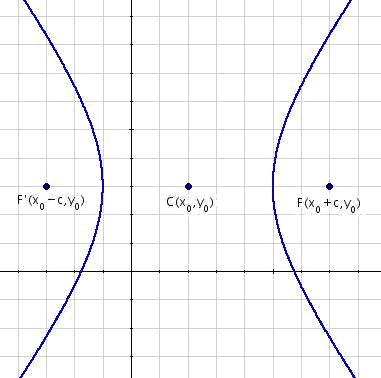
imagen

In this part we will deal with horizontal hyperbolas with the center in a generic point C(x0,y0).

The focal axis is parallel to the abscissa axis, and therefore the foci are in the coordinates F′(x0−c,y0) and F(x0+c,y0).

Applying these foci to the general definition of the hyperbola PF―−PF′―=2a we obtain the expression (x−x0+c)2+(y−y0)2−(x−x0−c)2+(y−y0)2=2a

On having added the root, and raising to the square: ((x−x0+c)2+(y−y0)2)2=(2a+(x−x0−c)2+(y−y0)2)2(x−x0+c)2+(y−y0)2=4a2+4a(x−x0−c)2+(y−y0)2++(x−x0−c)2+(y−y0)2(x−x0)2+2(x−x0)c+c2+(y−y0)2=4a2+4a(x−x0−c)2+(y−y0)2++(x−x0)2−2(x−x0)c+c2+(y−y0)2

Simplifying and dividing by four: 4(x−x0)c=4a2+4a(x−x0−c)2+(y−y0)2(x−x0)c=a2+a(x−x0−c)2+(y−y0)2

On having cleared the root and having squared again: (c(x−x0)−a2)2=(a(x−x0−c)2+(y−y0)2)2c2(x−x0)2−2a2c(x−x0)+a4=a2((x−x0)2+(y−y0)2c2(x−x0)2−2a2c(x−x0)+a4=a2((x−x0)2−2c(x−x0)+x2+(y−y0)2)c2(x−x0)2−2a2c(x−x0)+a4=a2(x−x0)2−2ac(x−x0)+a2c2+a2(y−y0)2c2(x−x0)2−a2(x−x0)2−a2(y−y0)2=a2c2−a4(c2−a2)(x−x0)2−a2(y−y0)2=a2(c2−a2)

We divide by a2(c2−a2) to obtain 1 on the right: (c2−a2)(x−x0)2a2(c2−a2)−a2(y−y0)2a2(c2−a2)=1(x−x0)2a2−(y−y0)2(c2−a2)=1

Applying the definition c2=a2+b2, b2=c2−a2 is replaced and we get the desired equation: (x−x0)2a2−(y−y0)2b2=1

Example

Find the equation of the hyperbola of center C(2,3), apex A(2,6) and focus F(2,7).

The focal distance c=7−3=4a=6−3=3 With c2=a2+b2, so b=c2−a2=16−9=7.

Substituting in (x−x02)a2−(y−y0)2b2=1 and identifying C(x0,y0), we prove (x−2)29−(y−3)27=1