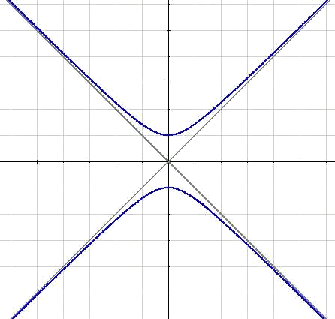
This hyperbola, in which $$a=b$$, is called equilateral. Hence the eccentricity is $$e=\sqrt{2}$$.
Multiplying by $$a^2$$ in the expression $$\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$, we get the equation $$x^2-y^2= a^2$$. In this case the asymptotes would be $$y=x$$, $$y =-x$$.
It is possible to observe that the asymptotes are orthonormals. It would then be interesting if they were to coincide with our orthonormal axes. To do so, all we need is a $$45$$ degree turn. The resultant equation $$x \cdot y=\frac{a^2}{2}$$ can be expressed as $$\displaystyle y=\frac{k}{x}$$ by generating the following diagram:

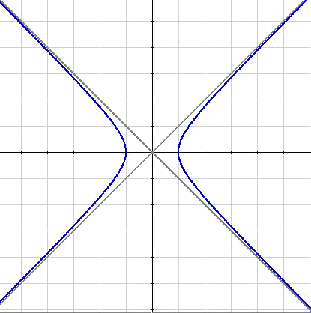
Another expression, in which the hyperbola will not be in the first quadrant anymore is $$\displaystyle y=-\frac{k}{x}$$, giving place to:

Consider the hyperbola $$y=-\frac{8}{x}$$, and find its eccentricity and its focal distance.
The eccentricity is, by definition, of an equilateral hyperbola $$e=\sqrt{2}$$.
To identify $$\displaystyle k=8=\frac{a^2}{2}$$, then $$a= \sqrt{16}=4$$.
As $$a=b$$, with $$c^2=a^2+b^2$$ is it $$c= \sqrt{2 \cdot a^2}=a\sqrt{2}=4\sqrt{2}$$.
