Hipèrbola equilàtera

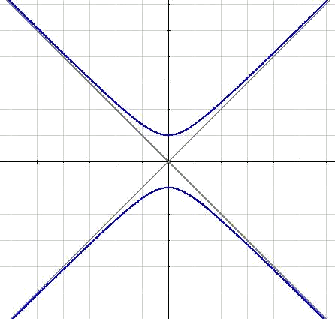
imagen

Es diu equilàtera a la hipèrbola on $a = b$ . D'aquí que l'excentricitat ha de valer $e = \sqrt{2}$ .

Multiplicant per $a^{2}$ en l'expressió $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ , s'arriba a l'equació $x^{2} - y^{2} = a^{2}$ . En aquest cas les asímptotes serien $y = x$ , $y = - x$ .

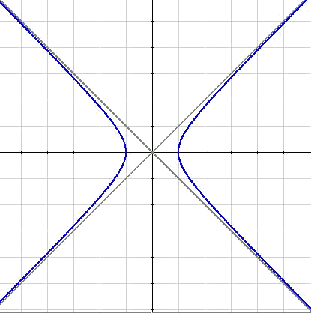
Es pot observar que les asímptotes són ortonormals. Seria llavors interessant que poguessin coincidir amb els nostres eixos ortonormals. Per arribar a això només cal un gir de $45^{\circ}$ . L'equació resultant $x \cdot y = \frac{a^{2}}{2}$ es pot expressar de la forma $y = \frac{k}{x}$ donant lloc a la figura següent:

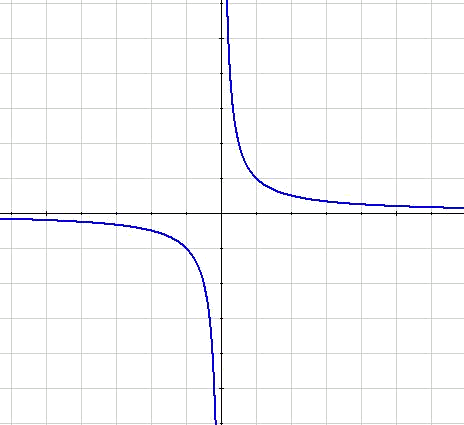
imagen

Una altra expressió, en la qual la hipèrbola ja no estarà en el primer quadrant és $y = - \frac{k}{x}$ , donant lloc a:

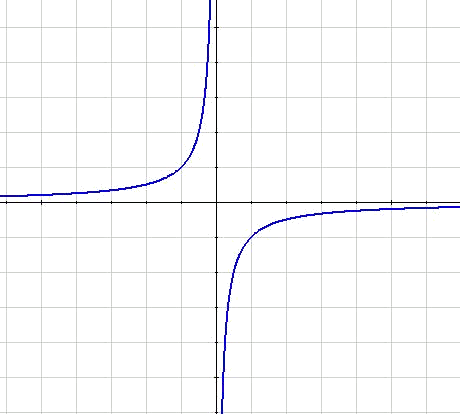
imagen

Exemple

Donada la hipèrbola $y = - \frac{8}{x}$ , trobar la seva excentricitat i la seva distància focal.

L'excentricitat és, per definició d'una hipèrbola equilàtera $e = \sqrt{2}$ .

Identificar $k = 8 = \frac{a^{2}}{2}$ , llavors $a = \sqrt{16} = 4$ .

Com que $a = b$ , amb $c^{2} = a^{2} + b^{2}$ es troba $c = \sqrt{2 \cdot a^{2}} = a \sqrt{2} = 4 \sqrt{2}$ .